호기심 많은 분석가
[BoostCamp] Week1_Day4. 길잡이, 마스터와의 만남 본문
부스트캠프
개발자의 지속 가능한 성장을 위한 학습 커뮤니티
boostcamp.connect.or.kr
개요
어느덧 흘러간 4일, 오늘은 우리 AI Math의 수업을 담당해주신 임성빈 마스터님과의 만남이 있었다. 어제에 이어 조금 더 활발해진 피어세션이 이루어졌다. 통계학에 대해서 학습했는데, 여러 번 느끼지만 통계학은 참 중요하고 남들과는 다른 강점을 여기서 가져야 하지 않을까? 모르는 개념은 조금 더 고민하고 여러 책을 찾아보자.
개인 학습
(AI Math 7강) 통계학 맛보기
모수가 뭐에요?
- 통계적 모델링은 적절한 가정 위해서 확률분포를 추정(inference)하는 것이 목표이며, 기계학습과 통계학이 공통적으로 추구하는 목표입니다.
- 그러나 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아낸다는 것은 불가능하므로, 근사적으로 확률분포를 추정할 수밖에 없다.
- 예측모형의 목적은 분포를 정확하게 맞추는 것보다 데이터와 추정 방법의 불확실성을 고려해서 예측의 위험을 최소화하는 것이다.
- 데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법을 모수적(parametric) 방법론이라고 한다
- Ex) 정규분포를 가진다고 가정한다. 평균과 분산이 굉장히 중요한 모수,
- 이 평균과 분산을 추정하는 방법을 모수적 방법론이라고 한다.
- 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌면 비모수(nonparametric) 방법론이라고 부른다
- 기계학습의 많은 방법론은 비모수 방법론에 속한다.
- 비모수 방법론이라고 해서 모수가 없는 것이 아니다. 무한히 많거나 유연하게 바뀌는 것뿐, 조심해야 함
확률분포 가정하기 : 예제
- 확률분포를 가정하는 방법 : 우선 히스토그램을 통해 모양을 관찰합니다.
- 데이터가 2개의 값(0 또는 1)만 가지는 경우 → 베르누이분포
- 데이터가 n개의 이산적인 값을 가지는 경우 → 카테고리분포
- 데이터가 [0,1] 사이에서 값을 가지는 경우 → 베타분포
- 데이터가 R 전체에서 값을 가지는 경우 → 정규분포, 라플라스 분포 등
- 기계적으로 확률분포를 가정해서는 안 되며, 데이터를 생성하는 원리를 먼저 고려하는 것이 원칙
- 각 분포마다 검정하는 방법들이 있으므로 모수를 추정한 후에는 반드시 검정을 해야 한다.
데이터로 모수를 추정해보자!
- 데이터의 확률분포를 가정했다면 모수를 추정해볼 수 있다.
- 정규분포의 모수는 평균 $\mu$와 분산 $\sigma^{2}$으로 추정하는 통계량(statistic)은 다음과 같다 :
- 표본평균들의 평균이 정규분포의 평균과 같다.
- 왜 N-1로 나누어주는가?
- 수학적 계산 & 자유도, 나머지 N-1개들로 1개가 추정되기 때문
- 왜 표본(샘플)의 분산에서는 n이 아닌 n-1로 나눌까?

- 통계량의 확률분포를 표집분포(sampling distribution)라 부르며, 특히 표본평균의 표집분포는 N이 커질수록 정규분포 $N(\mu, \sigma^2/N)$를 따릅니다.
- sample distribution과는 다른 것임. 주의
- 이를 중심극한정리(Central Limit Theorem)이라 부르며, 모집단의 분포가 정규분포를 따르지 않아도 성립합니다.
최대가능도 추정법
- 표본평균이나 표본분산은 중요한 통계량이지만 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라지게 됩니다.
- 이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나는 최대가능도 추정법(maximum likelihood estimation, MLE)입니다.
- $\hat{\theta}_{MLE}= \underset{\theta}{argmax}L(\theta;x)=\underset{\theta}{argmax}P(x|\theta)$
- 가능도는 주어진 데이터 x에 대해서 모수 $\theta$를 변수로 둔 함수로 해석하면 된다. 데이터가 주어진 상태에서 $\theta$를 변형시킴에 따라 값이 바뀌는 함수
- 가능도(likelihood) 함수는 모수 $\theta$를 따르는 분포가 x를 관찰할 가능성을 뜻하지만 확률로 해석하면 안 됩니다.
- 조건부확률 처럼 계산하지만, 다 더해서 1이 되거나 적분하였을 때 1이 되는 개념이 아니기에 확률로 해석하면 안 된다.
- $\theta$에 따른 크고 작은, 대소 비교만 해주면 된다.
- 데이터 집합 X가 독립적으로 추출되었을 경우 조건부확률들의 곱으로 MLE를 계산할 수 있는데, 이 경우 로그가능도를 최적화한다. → 로그의 성질을 이용하여 전체에 로그를 씌워주면 곱을 합으로 변환
- $L(\theta;X) = \prod_{i=1}^nP(x_i|\theta)\Rightarrow logL(\theta;X)=\sum_{i=1}^nlogP(x_i|\theta)$
왜 로그가능도를 사용하나요?
- 로그가능도를 최적화하는 모수 $\theta$는 가능도를 최적화하는 MLE가 된다.
- 둘 다 똑같다는 것
- 데이터의 숫자가 적으면 상관없지만 만일 데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로는 가능도를 계산하는 것은 불가능하다.
- 딥러닝, 머신러닝에 대한 설명들을 들으면 계산에 대한 어려움을 많이들 겪었음이 느껴진다. 대부분 연산량을 줄이기 위한 노력이 주를 이룸. 이번에도 같은 개념일 것
- 데이터가 독립일 경우, 로그를 사용하면 가능도의 곱셈을 로그가능도의 덧셈으로 바꿀 수 있기 때문에 컴퓨터로 연산이 가능해집니다.
- 경사하강법으로 가능도를 최적화할 때 미분 연산을 사용하게 되는데, 로그 가능도를 사용하면 연산량을 $O(n^2)에서\ O(n)$으로 줄여줍니다.
- 대게의 손실함수의 경우 경사하강법을 사용하므로 음의 로그가능도(negative log-likelihood)를 최적화하게 됩니다.
- 경사하강법은 목적식을 최소화하게 된다. 하지만 로그가능도의 경우 최댓값을 찾아주기에 최소화하기 위해 음의 로그가능도를 사용해준다.
최대가능도 추정법 예제 : 정규분포
- 정규분포를 따르는 확률변수 X로부터 독립적인 표본 ${ x_1, x_2, \cdots, x_n }$ 을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?

- 주어진 데이터를 가지고, 현재 수식과 같이 likelihood함수를 최적화하는 $\theta$를 찾는 것이다.
- 정규분포이기 때문에 2개의 모수를 가진다 - 평균과 분산
- 정규분포의 확률밀도함수이므로 식으로 변환해준 뒤 log로 풀어주고 계산하면 마지막 식이 도출된다.
- $\theta=(\mu,\sigma)$에 대해 마지막 수식을 미분해서 최적화를 할 수 있다.
- 두 미분이 모두 0이 되는 $\mu,\sigma$를 찾으면 가능도를 최대화하게 된다.
- MLE는 불편추정량을 보장하지는 않는다.
- 모수와 다른 추정량이지만, 통계량은 언제나 하나만 보장하지는 않음
- 그래도 최대가능도 추정법의 장점도 있으므로 사용

최대가능도 추정법 예제 : 카테고리 분포
- 카테고리 분포 Multinoulli($x; p_1, \cdots,p_d)$를 따르는 확률변수 X로부터 독립적인 표본 ${ x_1, x_2, \cdots, x_n }$을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?
- 카테고리 분포의 모수는 다음 제약식을 만족해야 한다. $\sum_{k=1}^dP_k=1$
- $x_{i,k}$는 0 또는 1의 값만 가지기에 $\sum_{i=1}^nx_{i,k}=n_k$
- $n_k$는 주어진 데이터 $x_i$ 대해서 k 값이 1인 데이터의 개수
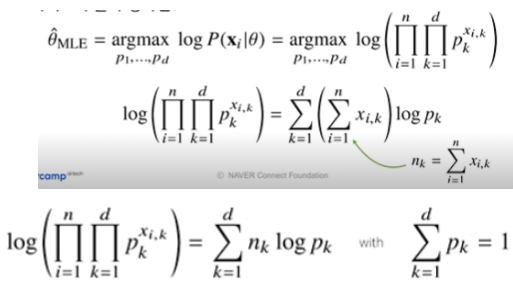
- 위 제약식을 가진 목적식을 최대화하는 것이 우리가 구하는 MLE이다.
- 목적식에 제약 식이 추가된 상황에서는 미분이 0이 되는 값을 구하는 것이 아니라 라그랑주 승수법을 사용해서 제약식에다가 라그랑주 승수에 해당하는 $\lambda$를 곱해줘서 식에다가 더해주어 해결할 수 있음
- 그다음 각각의 모수 $p_k$와 라그랑주 승수($\lambda$)에 대한 미분을 통해 최댓값을 찾음

- 결과 $p_k=\frac{n_k}{\sum_{k=1}^dn_k}$, 분모는 데이터 개수인 n을 의미한다.
- 위 식의 이해를 돕고자 참고, 위의 링크

- 그래서 카테고리 분포의 MLE는 경우의 수를 세어서 비율을 구하는 것
딥러닝에서 최대가능도 추정법
- 최대가능도 추정법을 이용해서 기계학습 모델을 학습할 수 있습니다.
- 딥러닝 모델의 가중치를 $\theta=(W^{(1)},\cdots,W^{(L)})$라 표기했을 때 분류 문제에서 소프트맥스 벡터는 카테고리분포의 모수 $(p_1, \cdots, p_k)$를 모델링합니다.
- 가중치를 거친 데이터가 소프트맥스 벡터에 대입이 되면 카테코리분포의 모수를 모델링한다.
- 원핫벡터로 표현한 정답 레이블 $y=(y_1,\cdots,y_k)$을 관찰 데이터로 이용해 확률분포인 소프트맥스 벡터의 로그가능도를 최적화할 수 있습니다.

확률분포의 거리를 구해보자
- 기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도합니다
- 데이터공간에 두 개의 확률 분포 P(x), Q(x)가 있을 경우 두 확률분포 사이의 거리(distance)를 계산할 때 다음과 같은 함수들을 이용합니다.
- 총변동 거리 (Total Variation Distance, TV)
- 쿨백-라이블러 발산 (Kullback-Leibler Divergence, KL)
- 이것에 대해 조금 더 살펴볼 것
- 바슈타인 거리 (Wasserstein Distance)
쿨백-라이블러 발산
- 쿨백-라이블러 발산(KL Divergence)은 다음과 같이 정의합니다.
- 좌항이 이산확률변수, 우항이 연속확률변수일 때의 수식을 의미한다.
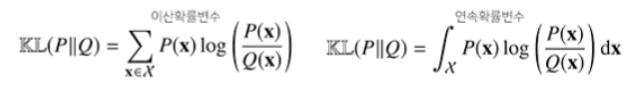
- 쿨백-라이블러는 다음과 같이 분해할 수 있습니다.
- x~P(x)는 x가 확률분포 P(x)에서 뽑혔다는 것
- 앞의 수식은 크로스 엔트로피, 뒤의 수식을 엔트로피라고 부름

- 분류 문제에서 정답레이블을 P, 모델 예측을 Q라 두면 최대가능도 추정법은 쿨백-라이블러 발산을 최소화하는 것과 같다.
- 거리를 최소화하는 것이 발산을 최소화하는 것과 같다.
총 정리
지금까지 데이터에서 통계학적인 방법에 의해서 기계학습에서 모수를 찾아보는 방법을 살펴봤다. 이 최대가능도를 통해서 모수를 추정하면서 정답레이블에 해당하는 확률분포와 모델이 추정하는 확률분포의 거리를 최소화하는 개념과 일치하고, 이걸 통해 기계학습 모형에서 통계학적으로 적절한 학습방법론을 사용한다는 원리를 배웠다.
앞으로 딥러닝, 머신러닝의 논문을 살펴보면 손실함수가 어떻게 나왔는지를 볼 때 MLE에서 많이 유도됐음을 확인할 수 있을 것이다.
(AI Math 8강) 베이즈 통계학 맛보기
- 베이즈 정리는 데이터가 새로 추가되었을 때 정보를 업데이트하는 방식에 대한 기반이 되므로 오늘날 머신러닝에 사용되는 예측모형의 방법론으로 굉장히 많이 사용되는 개념이다.
조건부 확률이란?
- 베이즈 통계학을 이해하기 위해선 조건부 확률의 개념을 이해해야 한다.
- 사건 B가 일어난 상황에서 사건 A가 발생할 확률을 의미한다.
- $P(A\cap B) = P(B)P(A|B)$
- 베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려준다.
- $P(B|A)=\frac{P(A\cap B)}{P(A)}=P(B)\frac{P(A|B)}{P(A)}$
- A라는 새로운 정보가 주어졌을 때 P(B)로부터 P(B|A)를 계산하는 방법을 제공한다.
베이즈 정리 : 예제
$P(\theta|\mathcal{D}) = P(\theta)\frac{P(\mathcal{D}|\theta)}{P(\mathcal{D})}$
- $\mathcal{D}$ : 새로 관찰하는 데이터
- $\theta$ : hypothesis, 모델링하는 event, 모델에서 계산하고 싶은 parameter(모수)
- $P(\theta|\mathcal{D})$ : 사후확률(posterior), 데이터를 관찰했을 때 이 parameter, hypothesis가 성립할 확률 - 관찰 이후에 도출하는 확률이기 때문에 사후확률이라 부름
- $P(\theta)$ : 사전확률(prior), 데이터가 주어지기 전에, $\theta$에 대한 모델링하기 전에 설정한 확률분포, 사전확률에서 사후확률을 계산할 때 베이즈 정리의 공식을 통해 업데이트한다.
- $P(\mathcal{D}|\theta)$ : 가능도(likelihood) 현재 주어진 paramter(모수), 가정에서 이 데이터가 관찰될 확률 계산
- $P(\mathcal{D})$ : Evidence, 데이터 전체의 분포
COVID-99(실수아님)의 발병률이 10%(사전확률)로 알려져있다. COVID-99에 실제로 걸렸을 때 검진될 확률은 99%(가능도), 실제로 걸리지 않았을 때 오검진(1종 오류)될 확률이 1%라고 할 때, 어떤 사람이 질병에 걸렸다고 검진결과가 나왔을 때 정말로 COVID-99에 감염되었을 확률은?
- 사전확률, 민감도(Recall), 오탐률(False alarm)을 가지고 정밀도(Precision)을 계산하는 문제이다
- $\theta$를 COVID-99 발병 사건으로 정의(관찰 불가)하고, $\mathcal{D}$를 테스트 결과라고 정의(관찰 가능)한다.
$P(\theta) = 0.1$, $P(\mathcal{D}|\theta)=0.99$, $P(\mathcal{D}|\neg\theta)=0.01$
이제 Evidence 계산이 필요. Marginal distribution을 통해 구할 수 있다.
$P(\mathcal{D})=\sum_{\theta}P(\mathcal{D}|\theta)P(\theta)=0.99\times0.1+0.01\times0.9(P(\neg\theta))=0.108$
만일 $P(\mathcal{D}|\neg\theta)$를 모른다면 이 문제는 풀기 어렵다.
따라서 결과는 $0.1\times\frac{0.99}{0.108}\approx0.916$이다.
- 만약 오검진될 확률(1종 오류)가 10%로 늘어난다면? 0.524
- 오탐율(False alarm)이 오르면 테스트의 정밀도(Precision)가 떨어진다.
조건부 확률의 시각화

- 데이터 분석의 성질에 따라 1종 오류를 줄여야 할지 2종 오류를 줄여야 할지 판단하는 게 굉장히 중요하다.
- 의료 문제에서 False Negative(2종 오류)가 굉장히 중요한 지표이다.
- 질병이 아니라고 진단 내렸으나 실제 질병일 경우
- 의료 문제에서 False Negative(2종 오류)가 굉장히 중요한 지표이다.
- 1종 오류는 어디에서 더 중요할까?
- 보안 쪽에서 중요할 것.
- 제약회사에서 신약을 개발했을 때
- 사전 확률 주어진 확률이고 이것이 없을 경우 베이즈 정리를 적용하기 힘들다. 임의로 설정해주는 경우도 있지만 신뢰도가 낮아짐
베이즈 정리를 통한 정보의 갱신
- 베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후 확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있습니다.
- 이 프로세스를 반복함으로써 데이터를 새로 관측할 때마다 hypothesis나 모델의 parameter를 업데이트함으로써 모델의 정확도를 높일 수 있다.

- 앞서 COVID-99 판정을 받은 사람이 두 번째 검진을 받았을 때도 양성이 나왔을 때 진짜 COVID-99에 걸렸을 확률은?
- 베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후 확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있습니다.
- 세 번째 검사에도 양성이 나오면 정밀도가 99.1%까지 갱신된다.

- 베이즈 정리의 굉장히 큰 장점은 데이터가 새롭게 들어올 때마다 사후 확률을 업데이트할 수 있는데, 그 사후 확률을 사용한 덕분에 유용한 테스트를 할 수 있다.
조건부 확률 → 인과관계?
- 조건부 확률을 유용한 통계적 해석을 제공하지만 인과관계(causality)를 추론할 때 함부로 사용해서는 안된다.
- 영향이 있는 건 맞지만 만능은 아님, 주의해야 한다. 실제로도 오류를 많이 발생시킴
- 데이터가 많아져도 조건부 확률만 가지고 인과관계를 추론하는 것은 불가능하다.
- 인과관계는 데이터 분포의 변화에 강건한 예측모형을 만들 때 필요하다.
- 단, 인과관계만으로는 높은 예측 정확도를 담보하기는 어렵다.
- 왼쪽 그림과 같이 인과관계를 고려하지 않고 조건부 확률만으로 모델을 만들었을 경우 테스트 데이터를 굉장히 높은 확률로 예측할 수 있지만, 데이터의 분포가 바뀌거나 시나리오가 바뀌었을 경우 낮은 예측정확도를 보인다.
- 오른쪽 그림과 같이 인과관계 기반 예측모형은 데이터 분포의 변화에는 강건하지만 높은 예측 정확도를 담보하지는 못한다.

- 인과관계를 알아내기 위해서는 중첩요인(confounding facotr)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야 한다.
- 아래 그림의 Z에 해당하는데, 만일 Z의 효과를 제거하지 않으면 가짜 연관성(spurious correlation)이 나온다. (우리는 T와 R의 인과관계가 궁금하다)
- 그렇게 되면 예측 모형의 정확도를 떨어트린다.

인과관계 추론 : 예제
- 신장 결석에 따라서 치료법을 선택할 것이다. 개복 수술, 주사 시술의 방법이 있는데 치료법에 따른 완치율의 원인과 결과 분석을 하고 싶다.
- 하지만 좀 전에 말했다시피 신장 결석 크기를 고려해주지 않으면 적절한 분석이 이루어지지 않는다.
- 전체적으로 B가 좋았지만 실제로는 둘 다 A가 완치율이 높음
- 이것이 바로 심슨의 역설
- 그래서 중첩 효과를 제거해야만 제대로 된 분석이 가능함
- 아래와 같이 원래 조건부 확률을 통해 계산했을 때는 A가 78%, B가 83%가 나왔지만, 신장결석 크기에 상관없이(중첩 효과를 제거하고) 인과관계를 계산했을 때는 A가 83.25%, B가 77.89%로 정반대의 결과가 나오게 된다.

- 그래서 단순히 조건부 확률로 계산을 하는 것은 위험하고, 데이터에서 실제로 추론할 수 있는 사실관계들, 데이터가 생성되는 관계들, 도메인 지식을 활용해서 변수들끼리의 관계를 실제로 파악해야만 인과관계의 추론이 가능하다. 그래서 데이터 분석을 할 때 인과관계를 제대로 파악하는 것이 강건한 데이터 분석을 할 때 중요하다.
(Python 4-1강) Python Object Oriented Programming
객체 지향 프로그램(Object-Oriented Programming, OOP)
- 객체 : 실생활에서 일종의 물건 속성과 행동을 가짐
- OOP는 속성은 변수(Variable), 행동은 함수(method)로 표현됨
Ex) 인공지능 축구 프로그램을 작성한다고 가정
- 객체 종류 : 팀, 선수, 심판, 공
- Action : 선수 - 공을 차다, 패스하다
- Attribute : 선수 - 선수 이름, 포지션, 소속팀
OOP는 설계도에 해당하는 클래스(class)와 실제 구현체인 인스턴스(instance)로 나눔
- 붕어빵 틀(Class), 붕어빵(인스턴스)
Class 구현하기 in Python
[상식] Python Naming Rule
- 변수와 Class명 함수명은 짓는 방식이 존재
- snake_case : 띄어쓰기 부분에 "_"를 추가, 뱀처럼 늘여 쓰기, 파이썬 함수/변수명에 사용
- CamelCase : 띄어쓰기 부분에 대문자, 낙타의 등 모양, 파이썬 Class명에 사용
Attribute 추가하기
- Attribute 추가는 **init,** self와 함께!
- _init은 객체 초기화 예약함수
# class : class 예약어, SoccerPlayer : Class 이름, object : 상속받는 객체명(안적어줘도 됨)
class SoccerPlayer(object):
# init을 쓰면 객체를 초기화하는 것으로 약속
# self.을 이용하여 변수를 초기화해준다
def __init__(self, name, position, back_number):
self.name = name
self.position = position
self.back_number = back_number- __는 특수한 예약 함수나 변수 그리고 함수명 변경(맨글링)으로 사용
- Ex) main, add, str, eq
class SoccerPlayer(object):
# 속성 정보를 넣기 위해서는 항상 __init__을 해주어야함
# 축구선수니까 name, position, back_number가 있음
def __init__(self, name : str, position : str, back_number : int):
# self.name은 self에 소속된 name, 거기에 할당되는 name은 parameter
self.name = name
self.position = position
self.back_number = back_number
# __str__이라는 것은 특수한 예약 함수로, print를 찍었을 때 바꾸어주는 함수
def __str__(self) :
return "Hello, My name is %s. My back number is %d"% \
(self.name, self.back_number)
# 이거를 abc+park로 실행하면 "sonpark"라고 출력되는 예약 함수
def __add__(self, other) :
return self.name + other.name
def change_back_number(self, new_number):
print("선수의 등번호를 변경합니다 : From %d to %d" %\
(self.back_number, new_number))
self.back_number= new_number
abc = SoccerPlayer('son', "FW", 7)
park = SoccerPlayer('park', "WF", 13)
# abc, park가 객체고 SoccerPlayer가 Class임, 당연히 abc와 kein은 다른 객체이다method 구현하기
- method(Action) 추가는 기존 함수와 같으나, 반드시 self를 추가해야만 class 함수로 인정됨
objects(instance) 사용하기
- self는 생성된 instance라고 부름
- Object 이름 선언과 함께 초기값 입력 하기
- jinhyun = SoccerPlayer("Jinhyun", "MF", 10)
객체명 Class명 init함수 Interface, 초기값
jinhyun = SoccerPlayer("Jinhyun", "MF", 10)
print("현재 선수의 등번호는 :", jinhyun.back_number)구현 가능한 OOP 만들기 - 노트북
- Note를 정리하는 프로그램
- 사용자는 Note에 뭔가를 적을 수 있다.
- Note에는 Content(str)가 있고, 내용을 제거(remove)할 수 있다.
- 두 개의 노트북을 합쳐 하나로 만들 수 있다.
- Note는 Notebook에 삽입된다.
- Notebook은 Note가 삽입될 때 페이지(Attribute)를 생성하며, 최고 300페이지까지 저장 가능하다.
- 300 페이지가 넘으면 더 이상 노트를 삽입하지 못한다.

Note Class
class Note(object):
def __init__(self, content=None):
self.content = content
def write_content(self, content):
self.content = content
def remove_all(self):
self.content = ""
def __add__(self, other) :
return self.content + other.content
def __str__(self):
return self.content
class NobeBook(object):
def __init(self, title):
self.title = title
self.page_number = 1
self.notes = {}
def add_note(self, note, page=0):
if self.page_number < 300 :
if page == 0 :
self.notes[self.page_number] = note
self.page_number += 1
else:
self.notes = {page:note}
self.page_number += 1
else :
print("Page가 모두 채워졌습니다.")
def remove_note(self, page_number):
if page_number in self.notes.keys():
return self.notes.pop(page_number)
else:
print("해당 페이지는 존재하지 않습니다")
def get_number_of_pages(self):
return len(self.notes.keys())OOP characteristic
객체 지향은 실제 세상을 모델링한 것 - 그래서 필요한 것들이 있다
- 상속, 다형성, 가시성
상속(Inheritance)
- 부모클래스로부터 속성과 Method를 물려받은 자식 클래스를 생성하는 것
# 부모 클래스
class Person(object):
def __init__(self, name, age):
self.name = name
self.age = age
# 자식 클래스
# Korean은 Person이라는 상속을 받았기 때문에
# Person의 속성을 사용할 수 있음
class Korean(Person):
pass
first_korean = Korean("Sungchul", 35)
print(first_korean.name) # Sungchulclass Employee(Person): # 부모 클래스 Person으로부터 상속
def __init__(self, name, age, gender, salary, hire_date):
super().__init__(name, age, gender) # 부모객체 사용
self.salary = salary
self.hire_date = hire_date # 속성값 추가
def do_work(self): # 새로운 메서드 추가
print("열심히 일을 합니다.")
def about_me(self): # 부모 클래스 함수 재정의
super().about_me() # 부모 클래스 함수 사용
print("제 급여는 ", self.salary, "원 이구요, 제 입사일은 ", self.hire_date, "입니다.")myPerson = Person("John", 34, "Male")
myEmployee = Employee("Daeho", 34, "Male", 3000000, "2012/03/01")
myPerson.about_me()
myEmployee.about_me()다형성(Polymorphsim)
- 같은 이름 메소드의 내부 로직을 다르게 작성
- Ex) draw(Rectangle), draw(Circle) : 메소드의 이름은 같지만 세부적인 구현이 다름
class Animal :
def __init__(self, name) :
self.name = name
def talk(self) :
# 아직 만들어지지 않음
raise NotImplementedError("Subclass must implement abstrack method")
class Cat(Animal):
def talk(self):
return "Meow!"
class Dog(Animal):
def talk(self):
return "Woof! Woof!"
# 인스턴스
animals = [Cat("Missy"),
Cat("Mr. Mistoffelees"),
Dog("Lassie")]
# 이게 가능
for animal in animals :
print(animal.name + ":" + animal.talk())가시성(Visibility)
- 객체의 정보를 볼 수 있는 레벨을 조절하는 것
- 누구나 객체 안에 모든 변수를 볼 필요가 없음
- 객체를 사용하는 사용자가 임의로 정보 수정
- 필요 없는 정보에는 접근할 필요가 없음
- 만약 제품으로 판매한다면? 소스의 보호
[알아두면 상식] Encapsilation
- 캡슐화 또는 정보 은닉 (Information Hiding)
- Class를 설계할 때, 클래스 간 간섭/정보공유의 최소화
- 심판 클래스가 축구선수 클래스 가족 정보를 알아야 하나?
- 캡슐을 던지듯, 인터페이스만 알아서 써야 함
Example1
- Product 객체를 Inventory 객체에 추가
- Inventory에는 오직 Product 객체만 들어감
- Inventory에 Product가 몇 개인지 확인이 필요
- Inventory에 Product items는 직접 접근이 불가
- 확인 및 수정 불가능
class Product(object):
pass
class Inventory(object):
def __init__(self):
self.__items = [] # __이것을 이용해 Private 변수로 선언, 타객체가 접근 못함
def add_new_item(self, product):
if type(product) == Product :
self.__items.append(product)
print("new item added")
else :
raise ValueError("Invalid Item")
def get_number_of_items(self):
return len(self.__items)my_inventory = Inventory()
my_inventory.add_new_item(Product())
my_inventory.add_new_item(Product())
my_inventoryExample2
- Product 객체를 Inventory 객체에 추가
- Inventory에는 오직 Product 객체만 들어감
- Inventory에 Product가 몇 개인지 확인이 필요
- Inventory에 Product items 접근 허용
class Inventory(object):
def __init__(self):
self.__items = []
# property decorator 숨겨진 변수를 반환하게 해줌
# 외부에서는 __items가 접근이 안되는데 내부에서는 접근 가능하게 만들어줌
@property
def items(self):
return self.__items
my_inventory = Inventory()
my_inventory.add_new_item(Product())
my_inventory.add_new_item(Product())
print(my_inventory.get_number_of_items())
# 마찬가지로 my_inventory.__items는 접근이 불가능하지만
items = my_inventory.items # Property decorator로 함수를 변수처럼 호출
items.append(Product())
print(my_inventory.get_number_of_items())decorate
decorate 이해에 앞서 3가지 개념을 알아보자 first-class objects, inner function, decorator
first-class objects
- 일등함수 또는 일급 객체
- 변수나 데이터 구조에 할당이 가능한 객체
- 파라미터로 전달이 가능 + 리턴 값으로 사용
그래서 파이썬의 함수는 모두 일급함수이다
def square(x):
return x*x
f = square # 함수를 변수로 사용
f(5)
def cube(x):
return x*x*x
# 함수를 파라미터로 사용 (method에 square나 cube를 사용)
def formula(method, argument_list) :
return [method(value) for value in argument_list]Inner function
- 함수 내에 또 다른 함수가 존재
def print_msg(msg):
def printer():
print(msg)
printer()
print_msg("Hello, Python")- closures : inner function을 return 값으로 반환
def print_msg(msg):
def printer() :
print(msg)
return printer
another = print_msg("Hello, Python")
another()# closure 사용 예제1
def tag_func(tag, text):
text = text
tag = tag
def inner_func():
return '<{0}>{1}<{0}>'.format(tag, text)
return inner_func
h1_func = tag_func('title', "This is Python Class")
p_func = tag_func('p', "Data Academy")decorator function
- 복합한 클로져 함수를 간단하게
def star(func): # <- 아래 @star 밑의 printer가 func로 전달 된다.
def inner(*args, **kwargs):
print("*" * 30)
func(*args, **kwargs)
print("*" * 30)
return inner
@star
def printer(msg):
print(msg)
printer("Hello")
******************************
Hello
******************************
def star(func):
def inner(*args, **kwargs):
print(args[1] * 30)
func(*args, **kwargs)
print(args[1] * 30)
return inner
@star
def printer(msg):
print(msg)
printer("Hello", "&")
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
Hello
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&def star(func):
def inner(*args, **kwargs):
print('*'*30)
func(*args, **kwargs)
print('*'*30)
return inner
def percent(func):
def inner(*args, **kwargs):
print('%'*30)
func(*args, **kwargs)
print('%'*30)
return inner
@star
@percent
def printer(msg):
print(msg)
printer('Hello')
******************
%%%%%%%%%%%%%%%%%%
Hello
%%%%%%%%%%%%%%%%%%
******************# decorator function
def generate_power(exponent): # <- exponent에 2
def wrapper(f): # <- f에 raise_two
def inner(*args):
result = f(*args) # <- *args에 n 입력7**2
return expoenent**result
return inner
return wrapper
# generator 자체에도 parameter를 입력할 수 있다.
@generate_power(2)
def raise_two(n):
return n**2
print(raise_two(7))
# 562949953421312 = 2**49(Python 4-2강) Module and Project
모듈(Module)
- 어떤 대상의 부분 혹은 조각
- Ex) 레고 블록, 벽돌, 자동차 부품들
- 프로그램에서는 작은 프로그램 조각들, 모듈들을 모아서 하나의 큰 프로그램을 개발함
- 프로그램을 모듈화 시키면 다른 프로그램이 사용하기 쉬움
- 카카오톡 게임을 위한 카카오톡 접속 모듈
- 파이썬의 Module==py 파일을 의미
- Import문을 사용하여 모듈을 호출
- 하지만 Import *는 문제가 된다. 모든 모델들을 메모리 안에 올리기 때문에 비효율적
- 어디의 어떤 함수가 쓰였는지 몰라 가독성이 떨어진다.
- 같은 이름을 가진 함수가 있을 경우 충돌이 벌어짐
Why is "import *" bad?
It is recommended to not to use import * in Python. Can anyone please share the reason for that, so that I can avoid it doing next time?
stackoverflow.com
패키지(Package)
- 모듈을 모아놓은 단위, 하나의 프로그램
- 하나의 대형 프로젝트를 만드는 코드의 묶음
- 다양한 모듈들의 합, 폴더로 연결됨
- init, main 등 키워드 파일명이 사용됨
- 다양한 오픈 소스들이 모두 패키지로 관리됨
폴더별로 init.py 구성하기
- 현재는 안 해줘도 되지만 원래는 없으면 패키지로 간주하지 않았음
- import와 all keyword를 사용하여
- 폴더를 만들 때는 init.py가 필수
최상단의 init.py 파일의 경우 모듈 이름들을 all에 적어줌

- 각 폴더별로 필요한 모듈을 구현함
# echo.py
def echo_play():
print("Hello Echo")# __init__.py <- game 폴더에 있음(최상단)
# 앞으로 사용할 폴더명을 적어줌
__all__ = ["image", "sound", "stage"]
from . import image
from . import sound
from . import stage
# 각각의 폴더마다 자신이 사용할 것을 기록해주는 것이 좋음
# 예를 들어 stage의 __init__.py 파일이라면
# 다른 폴더도 마찬가지
__all__ = ['main', 'sub']
from . import main
from . import sub- 그다음 최상단 game 폴더에 main.py 파일을 만들어줌
# __main__.py
from sound import echo
if __name_ == "__main__" :
print("Hello Game")
print(echo.echo_play())- 이렇게 main파일을 만들어두면 총 패키지 이름인 game을 python game이라고만 입력해도 "Hello Game"과 "Hello Echo"가 뜬다
[참고] package namespace
- Package 내에서 다른 폴더의 모듈을 부를 때 상대 참조로 호출하는 방법
from game.graphic.render import render_test # 절대 참조
from .render import render_test # .현재 디렉토리 기준
from ..sound.echo import echo_test # ..부모 디렉토리 기준가상환경 설정하기
대표적인 도구 virtualenv와 conda가 있음
virtualenv + pip
- 가장 대표적인 가상환경 관리도구
- 레퍼런스 + 패키지 개수
conda
- 상용 가상환경도구 miniconda 기본 도구
- 설치의 용이성
- Windows에서 장점
- Python의 경우 C로 이루어져 있는데 pip는 c로 complie이 안되어 있는 경우가 많다. 그래서 compile 된 코드가 함께 있는 conda가 Windows와 굉장히 잘 맞는다
피어세션
학습에 대한 내용에서 이해 안 가는 부분 외에도 분위기를 유하게 풀어가고자 떠오르는 궁금증들과 진로에 대한 이야기들도 나누면서 오늘 피어세션을 진행하였다.
Q1. 딥러닝에서 최대가능도 추정법 : 딥러닝 모델의 가중치를 θ = (W(1), ..., W(L))라 표기 했을 때 분류 문제에서 소프트맥스 벡터는 카테고리 분포의 모수 (p1,...,pk)를 모델링한다는 의미가 무엇인가?
A. pi들이 그 자체로 비율을 의미하는데, 그것을 소프트맥스를 통해 도출해준다.

Q1-1. 같은 페이지의 원핫벡터도 카테고리 분포를 따르는가?
A. 맞습니다. 그렇게 생각하시면 됩니다. 카테고리 분포를 모델링한다는 게 카테고리 분포에서 뽑혔다고 가정한다는 것이다.
Q2. 인과관계 나오기 전에 조건부확률로만 하면 안 되고 뭔가 인과관계추론을 해야 된다라고 설명을 해주셨는데 그러면 이 신장결석 예제에서 인과관계를 안 쓴 거는 뭐가 되는 걸까요? 그냥 조건부 확률만 보면
A. 신장결석 크기 자체가 요인이 아닌가요? 치료법 A랑 B만 있다면 완치율 같은 거는 A일 때 완치될 확률/ 안될 확률처럼 신장결석 크기를 추가하지 않은 overall이랑 비교해보시면 될 것 같습니다.
이다음부터는 살짝 편안한 대화에 가까웠다.
Q3. 의료 데이터에서는 2종 오류가 중요한데 그렇다면 1종 오류가 중요한 곳은 어디일까요?!
A. 틀린 것에 열리면 안 되니까 보안 데이터에서 중요하고, 신약을 개발할 때도 중요하다고 합니다. 효과가 있는 데 없다고 할 경우에는 회사의 돈만 손해를 보면 되는데, 효과가 없는 데 있다고 얘기한다면 굉장한 파장을 불러일으킬 수 있으니까요.
Q4. CV나 NLP에서 남들과는 다른 차별성을 갖기 위해선 어떤 강점을 어필할 수 있는가?
A. NLP에서는 국문학적 도메인이 굉장히 큰 강점이라 생각하지만, CV는 잘 모르겠습니다..
마지막으로 우리는 질문을 카톡을 통해 받았는데 슬랙에다가 올리는 것은 어떨까? 대화와 질문이 구분이 되어서 좋을 것 같다.
마스터 클래스
- 임성빈 유니스트 조교수님
- 2019년까지 KAKAO Brain 근무
- Casual Inference(인과관계모형) 데이터싸이언티스트는 알아두면 좋다.
똑똑하게 익숙해지는 방법
많이 보는 것보다 많이 사용하는 게 더 좋다!
- 용어의 정의(Definition)는 일단 외우는 것부터 시작합니다
- 교과서나 위키피디아를 활용하면 좋습니다.
- 만일 용어 사용이 헷갈린다면 인공지능 커뮤니티에 물어보세요!
- AI Korea(Deep Learning), PyTorch KR, TensorFlow KR - 주로 출몰 지역
- 용어를 외웠다면 예제를 찾아보도록 합시다.
- 가령 likelihood example을 구글링 해보면 위와 같은 설명 자료를 찾을 수 있습니다.
- 여러분의 문제에 어떤 수학을 적용할 것인가를 배우는 것이다. 수학자가 될 필요는 없다.
여러 모델들의 수학적 원리를 모두 이해하고 있어야 하나요?
- 모두 이해하는 것은 어렵지만 적어도 원리를 이해하는 데 필요한 기초를 갖춰야 합니다.
- 기댓값, likelihood같은 기초 개념들은 알고 있어야 한다.
어떤 분야가 기초일까?
- 선형대수/확률론/통계학은 꼭 알아두는 게 좋다.
- 기업 및 대학원 면접 때 정말 많이 물어봅니다
- 알고리즘이랑 최적화 내용도 같이 공부하면 시너지가 좋습니다.
- 머신러닝 이론을 공부할 게 아니라면 해석학/위상수학까지 공부할 필요는 없다.
- 기초 자체를 공부하기보다 머신러닝에서 어떻게 활용되는지 검색해보자
- 분류 문제에서 왜 cross-entropy를 손실함수로 사용하는가?
- Example들 찾아보기
- 분류 문제에서 loss function에서 무엇을 사용하는가
- 증명 공부할 게 아니라 Definition, Example 등을 구글링 해서 찾아보면 좋다
- 기초 공부는 기초에서 끝나는 게 아니라 걔네들을 어떻게 활용하는지 이해해야 완성!
- 분류 문제에서 왜 cross-entropy를 손실함수로 사용하는가?
- 책 추천 Dive into Deep Learning
- 수학 부분을 먼저 보고 딥러닝 내용을 쭉 훑어봐라
- 코드 예시도 많은데, 그대로 써보는 것도 추천 - 코드를 아는 게 중요하다.
Dive into Deep Learning - Dive into Deep Learning 0.17.0 documentation
Dive into Deep Learning — Dive into Deep Learning 0.17.0 documentation
d2l.ai
ML 엔지니어는 수학을 어느 정도 알아야 할까요?
- 필요한 걸 공부해서 빠르게 따라잡을 수 있을 만큼 알아야 합니다.
- 내가 여기에서 강점을 가짐을 어필하자.

추천시스템 공부할 때 알아야 할 내용이 있나요?
- Dive into Deep Learning 16장 내용을 보면 공부할 수 있다.
- Multi-Armed Bandit
- 최근엔 MAB도 중요한 테크닉으로 사용되니 공부해봐!
- 통계적인 기초가 중요함!
AI 분야에서 학석박 간에 어떤 차이가 있을까요?
- 분야마다 다르겠지만 전문성이 다르고 대중화되지 않은 영역은 학위과정이 중요할 수 있다.
- NLP, CV 같은 대중화된 분야가 아니라면, 논문을 읽고 해석하고 판단이 필요하기 때문에 학위가 필요해질 것
- 이 사람은 어떤 전문성을 가지고 있는가?
- 논문을 썼는가
- 이 분야의 중요한 코드나 시스템 라이브러리들 중 코드 공유되지 않은 것을 오픈소스로 공개해보았는가
- 코드가 공유가 안된 중요한 논문 : 구글 등, 비슷한 퍼포먼스를 보여줄 때
- 텐서플로우의 코드를 파이토치로 구현하는 것도 좋다.
- 인턴 같은 기회들로 인해 많이 본 케이스
- 레퍼런스 체크, 교수들의 추천, 많은 사람들의 추천
- 밑바닥부터 시작하는 딥러닝
심슨의 역설
- 그 외에도 통계의 오류
- 자주 범하는 실수에 대한 책
- The Book of Why: The New Science of Cause and Effect
Amazon.com
Enter the characters you see below Sorry, we just need to make sure you're not a robot. For best results, please make sure your browser is accepting cookies.
www.amazon.com
코드 구현
수학이든 모델이든 line-by-line으로 구현해보는 연습이 필요하다. 논문 구현 시 필요한 테크닉들을 line-by-line 구현해보면 좋다. 모든 걸 다 기초적인 모델로 공부하지는 말고, 가치 있는 중요한 것들은 직접 구현해보는 연습을 거쳐봐
- 라이브러리로 제공되는 것들은 굳이 하지 말고, 딥러닝 프레임워크에 들어가 있지 않지만 중요한 애들은 line-by-line으로 구현해보자.
논문을 읽다 보면 모델의 구조나 학습 방법이 명확하지 않은 경우가 있는 것 같은데요, 이런 논문을 구현함에 있어서 중요한 점은 무엇이 있을까요??
- 엔지니어의 상상력이 필요하다. 비슷한 상황에서 어떻게 해결했는지 찾아보자
- 구현하기 쉬운 논문부터 해보고, 다음은 어려운 논문으로 구현해보자
- 모르면 커뮤니티가 도움이 될 것이다.
역시 마스터님의 강의답게 깔끔했고, 캠퍼분들이 모두 궁금해하시는 부분들을 꼭 집어서 해결해주셨다. 다들 덕분에 많은 위안과 동기를 얻은 것 같다. 나로서도 굉장히 도움이 되는 강의였다고 생각한다.
[AI Tech]Daily Report
Naver AI Tech BoostCamp 2기 캠퍼 허정훈 2021.08.03 - 2021.12.27 https://bit.ly/3oC70G9
www.notion.so
'Coding > BoostCamp' 카테고리의 다른 글
| [BoostCamp] Week1_Day5. 한 주의 마무리 (2) (0) | 2021.08.09 |
|---|---|
| [BoostCamp] Week1_Day5. 한 주의 마무리 (1) (0) | 2021.08.08 |
| [BoostCamp] Week1_Day3. 예상치 못한 인연의 시작 (4) | 2021.08.05 |
| [BoostCamp] Week1_Day2. 평화롭지만 치열했던. (0) | 2021.08.04 |
| [BoostCamp] Week1_Day1. 긴 여정의 서막 (3) | 2021.08.03 |




