호기심 많은 분석가
[BoostCamp] Week1_Day3. 예상치 못한 인연의 시작 본문
부스트캠프
개발자의 지속 가능한 성장을 위한 학습 커뮤니티
boostcamp.connect.or.kr
개요
3일 차에 접어들면서 들을 것도 많고 과제도 점점 많아지고 내용도 조금 어려워지며 살짝 두려움에 떨고 있다. 오늘도 개인 학습 후에 피어세션에서 토의를 나눴는데, 생각보다 모르는 내용이 많아서 질문이 몇 개 이루어졌다. 피어세션 시간에서도 완벽히 해결되지 않아, 학습 종료 이후에도 찾아보면서 조금은 해결했다.
피어세션이 끝난 후 18-19시 피어세션이 피어씁니다라는 이벤트를 진행했는데, 이 이벤트가 굉장히 인상 깊었다. 자세한 내용은 아래에서 마저 다루겠다.
개인학습
(AI Math 5강) 딥러닝 학습방법 이해하기
- 비선형모델인 신경망(neural network)을 배워보자.
- 신경망을 분해해보면 선형모델과 비선형함수들의 결합으로 이루어져 있음
- 그에 앞서 선형 모델을 다시 집어보자
- 각 행벡터 $o_i$는 데이터 $x_i$와 가중치 행렬 W 사이의 행렬곱과 절편 $b$ 벡터의 합으로 표현된다고 가정하자.

- 각 행벡터 $o_i$는 데이터 $x_i$와 가중치 행렬 W 사이의 행렬곱과 절편 $b$ 벡터의 합으로 표현된다고 가정하자.

-
- 데이터가 바뀌면 결괏값도 바뀌게 된다. 이때 출력 벡터의 차원은 d에서 p로 바뀐다.
- $d$개의 변수로 $p$개의 선형모델을 만들어서 $p$개의 잠재변수를 설명하는 모델을 상상해볼 수 있다.
소프트맥스 연산
- 딥러닝을 가지고 문제를 풀 때 주어진 데이터가 어떤 class에 해당하는 문제를 분류 문제라고 함
- 소프트맥스(softmax) 함수는 모델의 출력을 확률로 해석할 수 있게 변환해주는 연산입니다. → 그래서 분류할 수 있는 것
- 분류 문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측한다.
- $softmax(o) = softmax(Wx+b)$
- 추론을 할 때는 원-핫(one-hot) 벡터로 최댓값을 가진 주소만 1로 출력하는 연산을 사용해서 softmax를 사용하지는 않음
- 학습을 할 때 softmax가 필요한 것
- $softmax(o) = (\frac{exp(o_1)}{\sum_{k=1}^pexp(o_k),\cdots, \frac{exp(o_p)}{\sum_{k=1}^pexp(o_k)}})$
- 벡터를 입력받으면 [0.7, 0.2, 0.1] 이렇게 출력해줘서 다중 분류에 사용한다.
- numpy에서 구현해줄 때는 분자에서 np.max(vec, axis=-1, keepdims=True)로 max값을 빼주는데, 이것은 너무 큰 데이터가 들어옴으로써 overflow를 방지하기 위함이다. 그래도 결과는 동일하게 출력됨
- 이러한 트릭을 이용하여, 소프트맥스가 아닌 다른 액티베이션 함수(활성 함수)를 사용하여 비선형함수를 도출할 수 있다.
- 소프트맥스와 활성함수의 차이는 소프트맥스는 출력물의 모든 값에 고려를 하여 출력한다면, 활성함수는 다른 주소의 출력값은 고려하지 않고, 해당 주소의 출력값만 신경 쓴다. 그래서 벡터를 인풋으로 받지 않고 실수값을 인풋으로 받음
- 선형모델로 나온 결과값을 활성함수 취해준 것을 잠재벡터(히든벡터)라고 부름
- 요런 벡터들이 뉴런이라고 불리는 애들이고 그것으로 이루어진 것을 뉴럴 네트워크, 신경망이라고 함.
Further Question
- 분류 문제에서 softmax 함수가 사용되는 이유가 뭘까?
- softmax 함수는 출력을 확률로 해석할 수 있게 변환해주는 연산이다. 따라서 softmax 함수를 사용한다면, 모델의 결과를 확률로 표현하여 분류 결과와 비교할 수 있게 됩니다.
- softmax 함수의 결과값을 분류 모델의 학습에 어떤 식으로 사용할 수 있을까요?
- softmax 함수의 결과인 예측값과 정답이라고 할 수 있는 실제값의 오차를 최소화하는 방법으로 학습에 사용할 수 있습니다.
활성함수가 뭐에요?
- 활성함수(activation function)은 $\R$ 위에 정의된 비선형(nonlinear) 함수로서 딥러닝에서 매우 중요한 개념입니다.
- 활성함수를 쓰지 않으면 딥러닝은 선형모형과 차이가 없습니다.
- 왜 그런가? 활성함수 없이 계속하여 선형모델만 쌓아주면 결국은 선형의 형태이다.
- 그것을 활성함수를 통해서 비선형으로 바꾸어줄 수 있는 것
- 왜 비선형으로 바꿔줘?
- 데이터의 복잡도가 높아지고 차원이 높아지게 되면 데이터의 분포는 단순 선형 형태가 아닌 비선형(Non-Linearity)를 가지기 때문입니다.
- 시그모이드(sigmoid) 함수나 tanh 함수는 전통적으로 많이 쓰이던 활성함수지만 딥러닝에선 ReLU 함수를 많이 쓰고 있다.
- 왜 ReLU를 많이 쓸까?
- Cost가 적게 든다.
- 정확성이 높다 (Sigmoid의 Vanishing Gradient 해결)
- 그래프에서 ReLU는 선형이 아닐까 하는 의심이 들 수 있지만, 대표적인 비선형함수로써 좋은 성질이 많이 있어서, 최근 많이 쓰이는 활성함수이다.
- ReLU로 어떻게 곡선 함수를 근사하는가?
- Multi-layer의 activation으로 ReLU를 사용하게 되면 단순히 Linear한 형태에서 더 나아가 Linear한 부분 부분의 결합 합성 함수가 만들어지게 된다.
- 학습 과정에서 Backpropagation할 때, 이 모델은 데이터에 적합하도록 fitting 된다. ReLU의 장점인 gradient가 출력층과 멀리 있는 layer까지 전달된다는 성질로 인하여 데이터에 적합하도록 fitting이 잘되게 되고 이것으로 곡선 함수에 근사하도록 만들어진다.
- ReLU로 어떻게 곡선 함수를 근사하는가?
- 왜 ReLU를 많이 쓸까?

- 신경망은 선형모델과 활성함수(activation function)를 합성한 함수이다.
- 활성함수 $ \sigma $는 비선형함수로 잠재벡터 $ z = (z_1,\cdots ,z_q)의 각 노드에 개별적으로 적용하여 새로운 $ H=(\sigma(z_1), \cdots, \sigma(z_n)) $ 를 만든다.

- x를 선형 모델을 이용하여 z로 출력하고, 거기에 시그마를 씌워줘서 H를 만든다. 그 H를 다시 한번 이용하여 선형변환해주게 되면, 이것을 2층(2-layers) 신경망이라 한다.

- 이것을 여러 개의 층으로 만든 것을 다층(multi-layer) 퍼셉트론(MLP-multi-layer-perseptron)이라고 부르고, 딥러닝의 기초가 된다.
- 시그마, 즉 활성함수는 모든 값에다가 적용이 되는 것이기에 기본적으로 H와 Z함수는 모양이 같고 시그마 값만 취해진 것이다.
- 이렇게 L개의 순차적인 신경망 계산을 순전파(forward propagation)이라 부른다.
- 순전파는 학습이 아니라 주어진 결과에 따라 출력을 내뱉는 것
왜 층을 여러 개를 쌓나요?
- 이론적으로는 2층 신경망으로도 임의의 연속함수를 근사할 수 있다.
- 이를 universal approximation theorem이라 부른다.
- 이론은 이론일 뿐, 실제적으로는 2층으로는 높은 성능을 내기 어렵다
- 층이 깊을수록 목적함수를 근사하는데 필요한 뉴런(노드)의 숫자가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능
- 하지만 층이 깊을수록 좀 더 복잡한 함수를 근사할 수는 있지만, 최적화가 쉽다는 이야기는 아니다. 층이 깊어질수록 딥러닝은 학습하기가 어려움 → 나중에 다시 다루겠다.
딥러닝 학습원리 : 역전파 알고리즘
- 굉장히 중요한 부분
- 딥러닝은 역전파(backpropagation) 알고리즘을 이용하여 각 층에 사용된 파라미터 ${W^{(\zeta)},b^{(\zeta)}}_{\zeta=1}^L$를 학습한다.
- 우리는 경사하강법을 적용할 때 선형모델의 계수 $\beta$에 해당되는 그레디언트를 계산해서 파라미터를 업데이트했다.
- 딥러닝에서도 똑같음
- 각 층에 존재하는 파라미터들에 대한 미분을 해서 파라미터 업데이트를 해야 한다.
- 행렬들의 원소들의 모든 개수만큼 경사하강법이 적용되게 됨
- 선형모델의 경사하강법보다 훨씬 더 많은 계산이 이루어지게 됨
- 그래서 딥러닝에서는 선형모델처럼 한 번에 모든 방향을 계산할 수는 없고, 역전파 알고리즘을 통해 역순으로 순차적으로 한 번씩 계산해주어야 함
- 역전파 알고리즘은 위층에 있는 그레디언트를 먼저 계산한 후 점점 밑에 층으로 가면서 그레디언트를 업데이트하는 방식이다.
- 각 층 파라미터의 그레디언트 벡터는 위층부터 역순으로 계산하게 된다. (By 연쇄법칙-Chain Rule)

- 역전파 알고리즘은 합성함수 미분법인 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation)을 사용한다.
- 아래 그림에 굉장히 중요한 말이 있다. 딥러닝에서 각 뉴런에 해당하는 값을 텐서라고 표현하게 되는데, 각각의 텐서 값을 메모리에 저장해주어야만 컴퓨터가 packpropagation 계산이 가능하다.
- 그래서 미분을 사용하기 때문에 역전파는 순전파에 비해 메모리를 많이 사용한다.

- 예제 : 2층 신경망 역전파 알고리즘
- 여기서 첫 번째 층에 해당하는 $W^{(1)}$에 대해서 경사하강법을 쓰고 싶으면 어떻게 그레디언트를 구해줄 수 있을까?
- $W^{(1)}$는 행렬이므로 각 성분에 대한 편미분을 구해야 한다.

(AI Math 6강) 확률론 맛보기
딥러닝에서 확률론이 왜 필요한가요?
- 딥러닝은 확률론 기반의 기계학습 이론에 바탕을 두고 있습니다.
- 기계학습에서 사용되는 손실함수(loss function)들의 작동 원리는 데이터 공간을 통계적으로 해석해서 유도하게 됩니다.
- 예측이 틀릴 위험(risk)을 최소화하도록 데이터를 학습하는 원리는 통계적 기계학습의 기본 원리이다.
- 회귀 분석에서 손실함수로 사용되는 L2-norm은 예측오차의 분산을 가장 최소화하는 방향으로 학습하도록 유도합니다.
- 분류 문제에서 사용되는 교차엔트로피(cross-entropy)는 모델 예측의 불확실성을 최소화하는 방향으로 학습하도록 유도합니다.
- 불확실성을 측정하기 위해서는 측정하는 방법을 알아야 하는데, 두 대상을 측정하는 방법을 통계학에서 제공하기 때문에 기계학습을 이해하려면 확률론의 기본 개념을 알아야 합니다.
확률분포는 데이터의 초상화라고 할 수 있다
- 데이터공간을 $X\times Y$라 표기하고 D는 데이터공간에서 데이터를 추출하는 분포다.
- 데이터는 확률변수로 (x, y) ~ D라 표기
- $(x, y) \in X \times Y$는 데이터공간 상의 관측 가능한 데이터에 해당함
이산확률변수 vs 연속확률변수
- 확률변수는 확률분포 D에 따라 이산형(discrete)과 연속형(continuous) 확률변수로 구분하게 됩니다.
- 데이터 공간 XxY에 의해 결정되는 것으로 오해를 하지만 D에 의해 결정된다.
- 이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링한다
- $P(X\in A) = \sum_{x\in A}P(X=x)$, 확률질량함수
- $P(X=x)$는 확률변수가 x 값을 가질 확률로 해석할 수 있다.
- 연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도(density) 위에서의 적분을 통해 모델링한다
- $P(X\in A)=\int_AP(x)dx$
- 우리의 수업 때는 이산형과 연속형만 다루지만, 모든 수가 이 두 가지로 분류되는 건 아니라는 걸 기억해두자.

- 빨간색 칸으로 나누면서 이산형 확률변수로 표현할 수 있음
- 결합분포(joint distribution)를 선정할 때는 원래 확률분포에 상관없이 선정할 수 있음
- 이산형이든, 연속형이든
- 모델링 방법에 따라 결정되는 것
- 컴퓨터를 가지고 분석을 하기 때문에 분포의 형태가 다르더라도 근사를 시킬 수 있는 방법이 있기 때문
- P(x)는 입력 x에 대한 주변확률분포(marginal distribution) y에 대한 정보를 주진 않습니다.
- $P(x) = \sum_yP(x, y)$, $P(x)=\int_yP(x,y)dy$
- 조건부확률분포 $P(x|y)$는 데이터 공간에서 입력 x와 출력 y 사이의 관계를 모델링합니다.
조건부확률과 기계학습
- 조건부확률 $P(y|x)$는 입력변수 x에 대해 정답이 y일 확률을 의미한다.
- 연속확률분포의 경우 $P(y|x)$는 확률이 아니고 밀도로 해석한다는 것을 주의하자
- 로지스특 회귀에서 사용했던 선형모델과 소프트맥스 함수의 결합은 데이터에서 추출된 패턴을 기반으로 확률을 해석하는데 사용됩니다.
- 분류 문제에서 softmax($W\phi+b)$은 데이터 x로부터 추출된 특징패턴 $\phi(x)$과 가중치행렬 $W$을 통해 조건부확률 P(y|x)을 계산합니다.
- x 대신 $\phi(x)$를 써도 됨
- 회귀 문제의 경우 연속형확률변수이기 때문에 조건부기대값 $E[y|x]$을 추정합니다.
- 조건부기대값은 우리가 사용하는 L2-norm을 최소화하는 함수와 일치한다.
- 우리가 원하는 목적에 따라 조건부기대값이 아닌 median, 중앙값을 쓰기도 한다.
- 딥러닝은 다층신경망을 사용하여 데이터로부터 특징패턴 $\phi$을 추출한다.
- 특징패턴을 학습하기 위해 어떤 손실함수를 사용할지는 기계학습 문제와 모델에 의해 결정된다. (RMSE, MSE, F1_score, ...)
기대값이 뭔가요?
- 확률분포가 주어지면 데이터를 분석하는 데 사용 가능한 여러 종류의 통계적 범함수(statistical functional)를 계산할 수 있습니다.
- 기대값(expectation)은 데이터를 대표하는 통계량이면서 동시에 확률분포를 통해 다른 통계적 범함수를 계산하는 데 사용됩니다.
- $E_{x\sim P(x)}[f(x)]=\int_\chi f(x)P(x)dx$, $E_{x\sim P(x)}[f(x)]=\sum_{x\in \chi} f(x)P(x)dx$
- 연속확률분포의 경우엔 적분을, 이산확률분포의 경우엔 급수를 사용한다.
- 기대값을 이용해 분산(Variance), 첨도(Skewness), 공분산(Covariance) 등 여러 통계량을 계산할 수 있다.
- 기대값 = 평균, 동일한 개념, 기계 학습에서는 조금 더 폭넓게 사용된다.
- 목적으로 하는 함수를 기댓값을 통해 여러 방면에서 해석할 수 있다.
몬테카를로 샘플링
- 기계학습의 많은 문제들은 확률분포를 명시적으로 모를 때가 대부분이다
- 확률분포를 모를 때 데이터를 이용하여 기대값을 계산하려면 몬테카를로(Monte Carlo) 샘플링 방법을 사용해야 한다
- $E_{x\sim P(x)}[f(x)]\approx \frac{1}{N}\sum_{i=1}^Nf(x^{(i)}), x^{(i)} \overset{i.i.d}{\sim} P(x)$
- 샘플링하는 방법을 알고 있다면, 타겟으로 하는 f(x)에다가 x에 샘플링한 데이터 $x^{(i)}$를 대입하고, 그 데이터들의 산술평균을 구해주면 기댓값과 근사한다.
- 몬테카를로는 이산형이든 연속형이든 상관없이 성립한다.
- 몬테카를로 샘플링은 독립추출만 보장된다면 대수의 법칙(law of large number)에 의해 수렴성을 보장한다.
- 몬테카를로 샘플링은 기계학습에서 매우 다양하게 응용되는 방법입니다.
몬테카를로 예제 : 적분 계산하기
- 함수 $ f(x) = e^{-x^2} $의 구간 [-1, 1] 상에서 적분 값을 어떻게 구할까?

- 굉장히 흥미로운 주제의 이야기
- 적분구간이 [-1, 1]이므로, 이 구간에서 균등 분포로 샘플링해주게 된다.
- 그렇게 되면 확률분포로 바꿔주기 위해서는 구간의 길이가 2니까, 적분값을 2로 나눠주게 되면 균등 분포를 사용하는 것과 동일한 적분에 해당됨 → 이 경우는 기댓값을 계산하는 것과 같으므로 몬테카를로 방법을 사용할 수 있다.
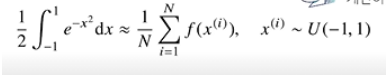
- 왼쪽 값을 구하는 것은 $e^{-x^2}$에다가 균등 분포에서 추출한 데이터를 집어놓고, 이 데이터의 산술평균을 구해주면 된다.
- 그러므로 문제의 적분값을 구하기 위해서는 방금 구한 산술평균에*2를 해주면 된다.
- 하지만 이것만으로는 이해가 조금 힘들 수 있다. 그래서 몬테 카를로를 소개한 다음의 링크를 보자
- 적분은 함수 곡선 아래 영역으로 해석될 수 있다.
- 구간 [a, b]가 존재하고, 그 사이 임의의 점 $x_i$를 취하면 f($x_i$)에 (b-a)를 곱한 임의의 사각형 영역을 얻을 수 있다. 이 무작위로 선택한 직사각형 평균 영역으로 적분 값을 근사하는 것이 몬테 카를로 통합이다.
- 문제는 샘플 개수가 너무 적으면 오차 범위가 커지므로 적절한 샘플 개수의 선택이 필요하다.
(Python 2-3강) Conditionals and Loops
- 프로그램 작성 시, 조건에 따른 판단과 반복은 필수
조건 참/거짓의 구분
- 숫자형의 경우는 수학에서의 참/거짓과 동일
- 컴퓨터는 존재하면 참 없으면 거짓이라고 판단함
- 그래서 1은 참, 0은 거짓
- All은 모든 것이 참이어야 True, 하나라도 아니라면 False 반환
- Any는 하나라도 True면 True
삼항 연산자(Ternary operators)
- 조건문을 사용하여 참일 경우와 거짓일 경우의 결과를 한 줄에 표현
value = 12
is_even = True if (value%2==0) else False
print(is_even) # True반복문
for vs while
- for문의 경우 주로 반복 횟수가 정해진 경우 배열과 함께 사용하고, while문은 무한루프나 특정 조건에 만족할 때까지 반복해서 사용할 경우 많이 사용한다. 둘 다 서로를 대체할 수 있지만 효율성을 위해 적절한 때에 사용한다.
Main
def main() :
print()
if __name__ == "__main__" :
main()
# 프로그램 실행시키면 if __name__ 가장 먼저 실행, 그래서 main함수부터
# if __name__이 없으면 파이썬 쉘에서 import 했을 때 바로 작동하지만.
# 있으면 그렇지 않고, 메인을 불러와야만 작동이 된다.(Python 2-4강) String and advanced function concept
다양한 문자열 표현
문자열 선언은 큰따옴표("")나 작은따옴표('')를 활용
It's OK라는 문자열은 어떻게 표현할까?
- word = 'It's OK'
- '은 문자열 구분자가 아닌 출력 문자로 처리
- word = "It's OK"
- 큰따옴표로 문자열 선언 후 작은따옴표는 출력 문자로 사용
두줄 이상은 어떻게 저장할까?
- \n : 줄 바꿈을 의미하는 특수 문자
- 큰따옴표 또는 작은따옴표 세 번 연속 사용
- '''It's OK
I'm Happy.
See you.'''
- '''It's OK
함수 호출 방식 개요
- 함수에서 parameter를 전달하는 방식
- 값에 의한 호출(Call by Value)
- 함수에 인자를 넘길 때 값만 넘김
함수 내에 인자 값 변경 시, 호출자에게 영향을 주지 않음
Ex) a=5, f(a) → f(5), 호출자는 a를 의미하고, f를 f(7)로 변환시키더라도 아무 영향이 없음 - 참조에 의한 호출(Call by Reference)
- 함수에 인자를 넘길 때 메모리 주소를 넘김(Like C의 Pointer)
함수 내에 인자 값 변경 시, 호출자의 값도 변경됨 - 객체 참조에 의한 호출(Call by Object Reference)

- 파이썬은 객체의 주소가 함수로 전달되는 방식
전달된 객체를 참조하여 변경 시 호출자에게 영향을 주나,
새로운 객체를 만들 경우 호출자에게 영향을 주지 않음
아래 사진을 참고하면 ham과 eggs는 둘 다 같은 주소를 참조하고 있었으나, 새로운 eggs를 할당해줌으로써 기존의 연결을 끊어버리고 새로운 연결로 할당
변수의 범위 (Scoping Rule) - global
- 함수 내에서 전역변수 사용 시 global 키워드 사용
def f() :
# 전역에서 선언된 s를 f 함수 내에서도 사용하겠다
global s
s = "I love London!"
print(s) # I love London!
s = "I love Paris!"
f()
print(s) # I love London!function type hints
- 파이썬의 가장 큰 특징 - dynamic typing
- 처음 함수를 사용하는 사용자가 interface를 알기 어렵다는 단점이 있음
- python3.5 버전 이후로는 PEP 484에 기반하여 type hints 기능 제공
- 늘 이게 뭔가 했는데 부스트 캠프 덕에 새로운 지식을 배워간다.
def do_function(var_name : var_type) -> return_type :
pass
def type_hint_example(name : str) -> str :
return f"Hello, {name}"- Type hints의 장점
- 사용자에게 인터페이스를 명확히 알려줄 수 있다
- 함수의 문서화 시 parameter에 대한 정보를 명확히 알 수 있다.
- mypy 또는 IDE, linter 등을 통해 코드의 발생 가능한 오류를 사전에 확인
- 시스템 전체적인 안정성을 확보할 수 있다.
- 나중에 만날 Pytorch의 코드인데, type hints가 활발히 쓰이는 것을 알 수 있다.

function docstring
- 파이썬 함수에 대한 상세 스펙을 사전에 작성 → 함수 사용자의 이해도 UP
- 세 개의 따옴표로 docstring 영역 표시 (함수명 아래)
- 함수, parameter, return에 대한 설명뿐만 아니라 example도 작성해주면 좋음
- VS code의 Extension에 Python Docstring Generator가 있다
- 굉장히 유용하니까 깔자. Ctrl+Shift+P 해서 Docstring 쳐주면 사용할 수 있음

함수 작성 가이드라인
- 함수는 가능하면 짧게 작성할 것 (줄 수를 줄일 것)
- 함수 이름에 함수의 역할, 의도를 명확히 드러낼 것
- 하나의 함수에는 유사한 역할을 하는 코드만 포함
- 아래의 경우 2번째 함수는 출력을 해줌으로써 사용자를 혼란에 빠트릴 수 있다.
- 위의 함수를 사용하자

- 인자로 받은 값 자체를 바꾸진 말 것 (임시변수 선언)
- 원래 변수를 바꿀 수도 있기 때문, 나에게 굉장히 필요한 습관

함수는 언제 만드는가?
- 공통적으로 사용되는 코드는 함수로 변환
- 복잡한 수식 → 식별 가능한 이름의 함수로 변환
- 복잡한 조건 → 식별 가능한 이름의 함수로 변환
파이썬 코딩 컨벤션
- 좋은 코드는 사람이 이해하기 좋은 코드다.
- 그러기 위해 규칙이 있는 데 그것을 코딩 컨벤션이라고 부른다
- 파이썬의 명확한 규칙은 없으나 구글의 Python Convention이라는 문서를 찾아보면 도움이 될 것
- 때로는 팀마다, 프로젝트마다 다르지만 일관성이 중요하다.
- 읽기 좋은 코드가 좋은 코드이다.
- 들여 쓰기는 공백 4칸을 권장하고, 한 줄은 최대 79자까지, 불필요한 공백은 피한다.
- = 연산자는 1칸 이상 안 띄움
- 주석은 항상 갱신, 불필요한 주석은 삭제
- 코드의 마지막에는 항상 한 줄 추가 (return 부분)
- 소문자 I, 대문자 O, 대문자 I 금지
- 함수명은 소문자로 구성, 필요하면 밑줄로 나눔
PEP8 - 파이썬 코딩 컨벤션의 기준
- flake8 모듈로 체크 가능하다.
- flake8 <파일명>
- conda install -c anaconda flake8
- 최근에는 flake8보다 black이라는 모듈을 사용해서 고친다
- black codename.py 명령을 사용, PEP 8에 맞춰서 자동 수정해줌

피어세션
강의 내용이 보다 조금씩 어려워지는 만큼 피어세션의 질문들도 어려워졌다. 사실 내가 궁금한 게 많은 편인데 정확히 알지 못해서 질문 내용도 구체적이지 않은 게 조금 아쉬웠다.
Q1. Activation function이 사용되는 이유가 무엇인가요?
A. 신경망을 아무리 깊게 쌓아도 Wx+b 연산만 반복하게 된다면 결과적으로 다중선형회귀 모형과 같은 결과가 도출된다. 선형연산에 activation function을 사용해줌으로써 비선형연산으로 만들어줄 수 있다.
Q2. 왜 ReLU 함수가 딥러닝에서 많이 사용되는가?
A. 역전파 시 레이어가 많으면 tanh는 그래디언트 벡터가 소실될 수 있고, 시그모이드 함수는 연산 cost가 커지기 때문에 그렇습니다. relu 함수는 미분 값이 0 혹은 1이기에 cost도 적고 gradient vanishing도 적습니다.
Q3. 몬테카를로 샘플링 예제에서 왜 $ \int e^{-x^2} $ 수식을 2로 나누어 주나요?
A. 위에서 설명했다시피 구간 [a, b]가 존재하고, 그 사이 임의의 점 $x_i$를 취하면 f($x_i$)에 (b-a)를 곱한 임의의 사각형 영역을 얻을 수 있다. 이 무작위로 선택한 직사각형 평균 영역으로 적분 값을 근사하는 것이 몬테 카를로 통합이다.
Q4. 최대가능도 추정법 예제 : 카테고리 분포 MLE 계산
A. 다들 이 계산에 대해서는 깔끔한 답이 돌아오지 않았다. 하루 뒤에 다시 토의하기로 함
제안사항
다음 주차 일정을 보고, 과제는 목요일까지 같이 끝내도록 정해보자
🌱 피어세션이 피어(Peer)씁니다
워낙 많은 사람들이 있다 보니 다른 조의 피어를 만날 수 있는 기회가 없었다. 그래서 부스트캠프 측에서 그 갈증을 해소할 수 있는 기회를 만들어주셨다. 피어세션이 피어(Peer)씁니다는 각 조별 소개 시간이었는데, 우리는 11-20조 들과 함께했다. 아래 사진처럼 사진과 태그들로 자신을 소개했고, 피어 규칙들을 뽐내는 시간이었다.
워낙 많은 조가 있어 모두 기억하지는 못했지만, 더러 기억에 남는 분들과 참고할만한 규칙들도 있었다. 우리는 그중 모더레이터가 해결되지 않은 질문을 정리해서 질문 게시판에 올리는 규칙을 추가했다. 😇

그다음은 예상치도 못했던 굉장히 흥미로운 사건이 발생했는데, 마지막 10분간은 랜덤 피어 스몰 토크를 진행하였다. 11-20조의 사람들이 랜덤으로 배정이 되었는데 너무 즐거웠다. 🤺 다들 유쾌하신 분들이 모여서 시간 가는 줄도 모르고 대화하다가 한 분이 감사하게도 슬랙에 새로운 그룹으로 만들어주셔서 다시 한번 인사를 나누고 우리 피어세션때 해결되지 않은 부분도 토의하고 소소한 꿀팁들도 나눴다. 역시 나는 새로운 사람을 만나는 게 정말 너무나도 즐겁다. 이것이 힐링이지..! 이 분들과의 좋은 인연이 계속 이어지면 좋겠다. :)

[AI Tech]Daily Report
Naver AI Tech BoostCamp 2기 캠퍼 허정훈 2021.08.03 - 2021.12.27 https://bit.ly/3oC70G9
www.notion.so
'Coding > BoostCamp' 카테고리의 다른 글
| [BoostCamp] Week1_Day5. 한 주의 마무리 (2) (0) | 2021.08.09 |
|---|---|
| [BoostCamp] Week1_Day5. 한 주의 마무리 (1) (0) | 2021.08.08 |
| [BoostCamp] Week1_Day4. 길잡이, 마스터와의 만남 (0) | 2021.08.06 |
| [BoostCamp] Week1_Day2. 평화롭지만 치열했던. (0) | 2021.08.04 |
| [BoostCamp] Week1_Day1. 긴 여정의 서막 (3) | 2021.08.03 |




