호기심 많은 분석가
[BoostCamp] Week1_Day1. 긴 여정의 서막 본문
부스트캠프
개발자의 지속 가능한 성장을 위한 학습 커뮤니티
boostcamp.connect.or.kr
개요
장장 5개월의 교육, 부스트캠프 AI Tech가 시작되었다. 첫날이라 굉장히 우여곡절도 많고 프로그램도 많았는데 앞으로 많이 성장하겠구나를 느꼈다. 타운홀 미팅으로 시작하여 밋 업을 거쳐 피어세션과 어색하DAY로 마무리 지어졌다. 기본적인 시간표는 오전 10시부터 오후 7시까지다.
공지와 출석, 질의응답은 슬랙(Slack)을 통해, 수업과 출석은 boostcourse, 협업은 Colab, Github, Notion, 카카오톡으로 이루어질 듯하다.
타운홀 미팅
타운홀 미팅이란 교육 도중에 전체 공지를 구두로 전달하는 시간인데 앞으로도 종종 한다고 함. 앞으로의 일정을 다시 복기하고 출석 방법등에 대해 소개받은 뒤 마스터 분들의 한 말씀을 듣고 Q&A 시간을 가졌다. 되게 인상 깊은 말이라 여기에도 남겨보고자 한다.
여러분들이 어떤 사람인지, 오늘 한번 작성해보세요. 나는 어떤 사람이고, 왜 이 과정에 참여했는지, 그리고 나는 어떤 사람이 되고 싶고, 어떤 분야에서 일하고 싶은지, 내가 현재 알고 있는 지식은 무엇인지 고민해보세요. 그리고 그것을 매달 새로 쓰며 회고해보세요. - 쏘카 데이터 그룹 팀장 변성윤
이 프로그램은 굉장히 수준 높은 프로그램이다. 그래서 많은 걸 배울 수 있을텐데 그중에서도 협업과 정보의 공유를 여기에서 많이 배워갔으면 좋겠다 - Upstage 김성훈
사실 데이터로 이야기하는 것이 너무 좋아서 이 공부를 시작했지만, 면접에서 미래의 목표나 모습을 물어보면 잘 대답 못할 때가 많았다. 아직까지도 제대로 모르겠기도 하고, 시간을 들여 나를 돌아보는 시간을 가져보자.🙂
밋 업
랜덤으로 배정 받은 5명의 팀원과 서로 알아가고 앞으로의 학습에 관한 그라운드 룰을 정하는 시간이었다. 1분을 제외하고는 다들 나와 나이가 비슷했고, CV에 관심 있는 분들이 많았다. 생각보다는 대화가 잘 이루어졌고 아래와 같은 룰을 설정하게 되었다.
팀명 : CV조
모더레이터 : 하루마다 변경 [오주영 → 허정훈 → 이준혁 → 조현동 → 황원상 → 임성민 순서]
매주 월요일 강의량을 보고 최소 학습량을 정하자.
그것을 피어세션 때 질의응답, 된다면 리뷰까지.
이번 주는 AI Math를 하루에 2 강의씩 리뷰하는 걸로 공부는 각자, 피어세션만 공유하는 걸로
💻협업 툴: 깃허브 & 노션, zoom
👨🎓각자 할 것
학습내용 정리 수업 듣고 궁금한 점 및 이해 되지 않는 내용 기록
→ 카톡이나 슬랙을 이용하여 공유 과제 제출 후: 코드 피어 리뷰
👨⚖️ 모더레이터 할 것
피어세션에서 있었던 질문과 답변 기록
💡 피어 규칙
피어세션에 참여 못할 경우 전날 자정 전까지 말하기 (자신이 모더레이터인 경우 대타도 구하기)
무단 불참 1번째 기프티콘 5000원 이하/1인 무단지각(5분 초과)
3번째 기프티콘 5000원 이하/1인
팀명을 다들 CV에 관심이 있고, 12조였기에 비슷한 CV조로 하자는 의견은 정말 크리에이티브했다. 멋진 팀원..!
피어세션 내용은 함께 공유하는 것이 좋기에 Notion으로 협업하게 되었다. (Notion의 Share 인원 제한이 5명뿐이라서 유료 계정을 가진 팀원 덕분에 진행할 수 있었다.) 각자 공부를 하면서 모르는 부분을 미리 카톡에 올려서 피어세션 때 논의하기로 했는데 되게 좋은 방법이라고 생각한다.
개인 학습
이번주의 강의는 프리코스에서 이미 학습했던 것을 과제와 함께 다시 복습하는 것이다. 그래서 그때의 정리를 다시 가져오자.
(AI Math 1강) 벡터가 뭐예요?
- 벡터는 숫자를 원소로 가지는 리스트(list) 또는 배열(array)입니다.
- 벡터의 개수를 차원이라고 한다.
- 세로 : 열벡터, 가로 : 행벡터
- 벡터는 공간에서 한 점을 나타냅니다.
- 벡터는 원점으로부터 상대적 위치를 표현합니다.
- 벡터에 숫자(스칼라)를 곱해주면 길이만 변합니다.
- 스칼라가 0보다 작으면 반대 방향이 된다.
- 벡터끼리 같은 모양을 가지면 연산이 가능하다
- 성분곱(Hadamard product)도 계산 가능 - element끼리의 곱 (x*y)
- 두 벡터의 덧셈은 다른 벡터로부터 상대적 위치 이동을 표현합니다.
벡터의 노름 구해보기
- 벡터의 노름(Norm)은 원점에서부터의 거리를 말합니다.
- L1-norm : $\lVert x \rVert_{1} = \sum_{i=1}^{d}|x_i|$, L2-norm : $\lVert x \rVert_{2} = \sqrt{\sum_{i=1}^{d}|x_i|^2}$
- 왜 다른 노름을 소개하는가?
- 노름의 종류에 따라 기하학적 성질이 달라진다.
- 머신러닝에선 각 성질들이 필요할 때가 있으므로 둘 다 사용합니다.
- L1 norm : 로버스트 회귀, 라쏘(Lasso) 회귀
- L2 norm : 라플라스 근사, 릿지(Ridge)
- 원이란 중점에서 일정한 거리의 점들의 집합을 의미한다.

- 벡터 사이의 거리를 계산해보자
- 두 벡터 사이의 거리를 계산할 때는 벡터의 뺄셈을 이용한다.
- L2 norm을 사용하면 제2 코사인 법칙에 의하여 각도로 계산 가능
- 다차원에서도 가능하다.
- L1 norm에서는 안 됨
내적은 어떻게 해석할까?
- 내적은 정사영(orthogonal projection)된 벡터의 길이와 관련 있다.
- Proj(x)의 길이는 코사인 법칙에 의해 $\lVert x \rVert cos{\theta}$가 된다.
- 내적은 정사영의 길이를 벡터 y의 길이 $\lVert y \rVert$만큼 조정한 값이다
- 두 벡터의 유사도(similarity)를 측정하는 데 사용
(AI Math 2강) 행렬이 뭐예요?
- 행렬(Matrix)은 벡터를 원소로 가지는 2차원 배열이다
X = np.array([1, -2, 3],
[7, 5, 0],
[-2, -1, 2])
# numpy에서는 행(row)이 기본 단위이다.- 전치행렬(transpose matrix)은 행과 열의 인덱스가 바뀐 행렬을 말합니다
- $X^T = (x_{ji})$
- 벡터가 공간에서 한 점을 의미한다면 행렬은 여러 점들을 나타낸다.
- 행렬의 행벡터 $x_i$는 i번째 데이터를 의미한다.
- Numpy에서 행렬 곱셈은 X@Y를 사용한다.
행렬도 내적이 있을까?
- 넘파이의 np.inner는 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다. $XY^T$
- 수학에서 말하는 내적($tr(XY^T)$)과는 다르므로 주의하자!
- 행렬은 벡터 공간에서 사용되는 연산자(operator)로 이해한다.
- 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다.
- 우리는 한 작업을 다른 차원에서 이야기하고 싶을 때가 있다. 그럴 때 행렬을 사용해주면 그 작업이 이루어지게 될 것.
- 행렬곱을 통해 패턴을 추출할 수 있고 데이터를 압축할 수도 있다.
- 이러한 변환을 선형변환(linear transform)이라 하고, 모두 행렬곱으로 계산할 수 있다.

- 어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix)라 부르고, $A^{-1}$라 표기한다.
- 역행렬을 1. 행과 열 숫자가 같고, 2. 행렬식(determinant)가 0이 아닌 경우에만 계산할 수 있다.
- np.linalg.inv(X)를 통해 구할 수 있음 - 이건 미리 알았으면 좋았을 텐데..
- 만일 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 $A^{+}$을 이용한다
- 얘는 차원이 달라도 괜찮음
- $n\geq m인\ 경우 A^+ = (A^TA)^{-1}A^T$
- $n\leq m인\ 경우 A^+ = A^T(AA^T)^{-1}$
- np.linalg.pinv(Y)로 구할 수 있음
- 원래 변수의 개수가 식의 개수보다 많으면 해가 무한하고 구할 수 없다
- 이때 그 해 중 하나를 무어-펜로즈 역행렬을 통해 구할 수 있다.
- np.linalg.pinv를 이용하면 연립방정식의 해를 구할 수 있다.

- 반대로 데이터가 변수 개수보다 많거나 같을 때
- 점들을 데이터로 표현하여 선형회귀 식을 찾을 때 그 coefficient를 무어-펜로즈 역행렬을 통해 구할 수 있다.
- np.linalg.pinv를 이용하면 데이터를 선형모델(linear model)로 해석하는 선형회귀식을 찾을 수 있다.

- sklearn의 LinearRegression과 같은 결과를 가져올 수 있다.
- 근데 같은 방법인데 결과가 다르게 될 때가 있다. 왜 일까?
- sklearn에서는 y절편을 스스로 추정하는 반면에 Moore-Penrose에서는 우리가 y절편(intercept)을 직접 추가해줘야 하기 때문
피어세션
팀을 이루어 함께 토의하고 상호 피드백하는 학습 활동으로써 부스트캠프에서도 핵심이 되는 활동이다. 오늘은 Math 1,2강에 대해서만 이야기 나누고자 하였지만 3,4강 내용도 조금은 추가되었고, 시간이 많이 남아 사담을 나눴다. 다들 어려워하지 않는 내용이라 그랬던 것 같고, 앞으로는 점점 내용이 어려워질 테니 이 시간들이 부족해지겠지.
하지만 쉽다고 느낀 것치곤 캠퍼분들의 질문들은 날카로웠고 다시금 생각하는 계기가 되었다.
Q1. Norm에 따라서 왜 원의 모양이 마름모 꼴이 나오기도 하는가?
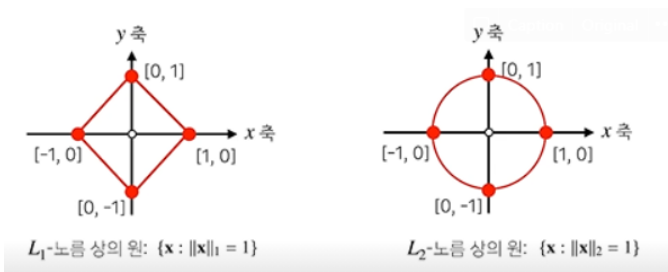
A. 원의 정의를 다시 떠올려볼까요? 원이란 평면 위의 한 점에서 이르는 거리가 일정한 평면 위의 점들의 집합으로 정의되는 도형입니다. 따라서 L1-norm에서의 거리는 좌표의 절댓값들의 합이기 때문에 마름모의 형태이지만 원이라고 부릅니다.
원 (기하학) - 위키백과, 우리 모두의 백과사전
기하학에서, 원(圓, 영어: circle)은 평면 위의 한 점에 이르는 거리가 일정한 평면 위의 점들의 집합으로 정의되는 도형이다. 이러한 점을 원의 중심이라고 하고, 중심과 원 위의 점을 잇는 선분
ko.wikipedia.org
Q2. 경사하강법 도출하는 법
오른쪽 상단의 식에서 하단의 식을 어떻게 하면 좀 쉽게 도출할 수 있을까요?
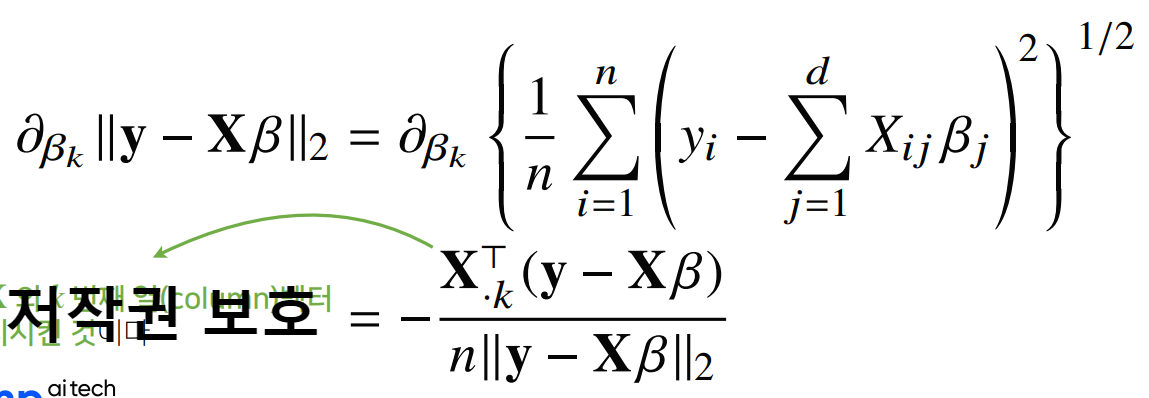
A. {} 안에 있는 식을 합성함수 f(x)라고 치환하고 Chain Rule을 이용하여 계산해주면 조금 더 쉽게 도출할 수 있습니다. 이해를 돕기 위하여 3x3 행렬을 통해 직접 계산해보시는 걸 추천드려요!
경사하강법
미분 미분이란? 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 가장 많이 사용하는 기법 수치 미분 전방 차분 이렇게 구현을 하게 되면 h가 아무리 작은 수라도 오차
velog.io
Q2-1. 위의 식에서 왼쪽 항과 오른쪽 항은 1/n 때문에 다릅니다. 이건 왜 존재하는 것인가요?
A. 사실 이것에 대한 명확한 답은 저도 모르겠습니다. 문의해볼 예정인데 다음 링크를 참조하면 이러한 이유로 볼 수 있다고 합니다.
저 식에서의 L2-norm은 수학의 L2-norm과는 풀이 방식이 살짝 다르다. 여기서 사용하는 L2-norm은 모델 학습에 사용되는 것이므로, n개의 데이터셋을 가지고 있다는 가정하에 출발한다. 따라서 바로 루트를 씌워주는 것이 아니라, 1/n로 평균 내준 뒤에 씌워준다.
경사하강법(Gradient Descent)의 기초와 이해
AI Math by 임성빈 교수님, BoostCamp AI Tech 2주차
blogik.netlify.app
→ 심지어 우리는 저 식의 최솟값을 찾는 것이 목적이기에 모두 같은 1/n으로 나눠줘도 학습에는 아무런 문제가 없다. 늘 머신러닝에서 그러듯이, 속도와 연산량을 낮춰주기 위해서는 1/n으로 나누는 것이 더 합리적이다.
추가 답변 게재
문의 결과 친절한 튜터님의 대답이 돌아왔다. 이런 것이 진짜 부스트캠프의 매력이 아닐까? 빠져들어.. 멘토님 사랑합니다..😘
결론적으로는 RMSE를 종종 L2-norm으로 써서, 원래 저 식은 RMSE를 묻는 건데 표기만 L2-norm처럼 됐다고 생각하면 좋을 듯하다.

Q3. A에 상관없이 항상 유사역행렬은 존재하는가?
- 만일 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 $ A^T $을 이용한다

A. 사실 답하기에 앞서 뒤통수를 한 대 맞은 듯 충격적인 질문이었다. 나는 왜 이걸 궁금해하지 않았지? 이런 항상 의심하는 비판적인 사고가 중요한 데 반성하자. 질문의 요지는 행렬 A가 nXm 행렬인데, 각각의 컬럼들이 선형독립이 아니라 하더라도 유사역행렬은 항상 구할 수 있는가였다. 우선 정답은 그렇다이다.
임의의 A에 대해서 유사역행렬은 항상 존재하지만, 위의 식을 만족시키는 $ A^+ $가 존재하기 위해서는 A의 열벡터가 모두 선형 독립 이어야 한다.
무어-펜로즈 유사역행렬 - 위키백과, 우리 모두의 백과사전
선형대수학에서, 무어-펜로즈 유사역행렬(Moore-Penrose疑似逆行列, 영어: Moore–Penrose pseudoinverse matrix)은 모든 모양의 행렬에 대하여 정의되는 연산이며, 가역 행렬의 역행렬 연산을 일반화한다.[1]:
ko.wikipedia.org
추가로 어색하DAY라는 앞으로 함께할 멘토분들을 소개받는 자리가 있었고, CV와 NLP를 고민하는 많은 사람들에게 도움을 준 시간이었다. 필수 과제와 필수 퀴즈들도 몇 개 나왔는데, 아직까지는 쉬운 난이도라 re함수를 사용해서 어렵지 않게 해결할 수 있었다.
이렇게 부스트캠프의 첫날이 지나갔다. 되게 쉽다고 생각한 내용에서도 답변이 어려웠는데 나중 가면 정말 머리 아프겠구나라는 걱정도 들고, 역시 여러 명이 같이 작업하다 보니 많은 의견들이 제시돼서 즐겁기도 했다. 내일은 면접 때문에 출석이 곤란한데 공가 처리가 잘 되길 바라야지. 다들 화이팅하시고 내일 뵙겠습니다. :)
[AI Tech]Daily Report
Naver AI Tech BoostCamp 2기 캠퍼 허정훈 2021.08.03 - 2021.12.27 https://bit.ly/3oC70G9
www.notion.so
'Coding > BoostCamp' 카테고리의 다른 글
| [BoostCamp] Week1_Day5. 한 주의 마무리 (2) (0) | 2021.08.09 |
|---|---|
| [BoostCamp] Week1_Day5. 한 주의 마무리 (1) (0) | 2021.08.08 |
| [BoostCamp] Week1_Day4. 길잡이, 마스터와의 만남 (0) | 2021.08.06 |
| [BoostCamp] Week1_Day3. 예상치 못한 인연의 시작 (4) | 2021.08.05 |
| [BoostCamp] Week1_Day2. 평화롭지만 치열했던. (0) | 2021.08.04 |




