호기심 많은 분석가
[이것이 취업을 위한 코딩 테스트다 with 파이썬] (한빛미디어, 나동빈) Chapter3. 그리디 본문
[이것이 취업을 위한 코딩 테스트다 with 파이썬] (한빛미디어, 나동빈) Chapter3. 그리디
DA Hun 2021. 4. 14. 22:45포스팅 개요
'혹시나 책에 있을 모든 실수와 오류는 온전히 제 책임이며, 책에 실린 좋은 아이디어와 표현은 모두 리뷰어님들의 조언 덕분입니다. 정말 고맙습니다.'라는 지은이의 글은 나동빈 저자님의 인품을 느낄 수 있는 한 줄이었습니다.
저도 저런 마인드를 가진 사람이 되겠다고 다짐하며 책과의 여정을 떠나보겠습니다.

포스팅 본문
그리디(Greedy) 알고리즘은 단순하지만 강력한 문제 해결 방법이다. 어떠한 문제가 있을 때 단순 무식하게, 탐욕적으로 문제를 푸는 알고리즘이다. 여기서 탐욕적이라는 말은 '현재 상황에서 지금 당장 좋은 것만 고르는 방법'을 의미한다.
- 특징 : 사전에 외우고 있지 않아도 풀 수 있는 가능성이 높은 문제 유형
- 코딩 테스트에서 출제되는 그리디 알고리즘 유형의 문제는 창의력, 즉 문제를 풀기 위한 최소한의 아이디어를 떠올릴 수 있는 능력을 요구함.
- 특정한 문제를 만났을 때 단순히 현재 상황에서 가장 좋아 보이는 것만을 선택해도 문제를 풀 수 있는지를 파악할 수 있어야 함
본 코드는 모두 제 Github에 올려두었습니다. (https://github.com/herjh0405/Coding_Test)
3-1. 거스름돈
당신은 음식점의 계산을 도와주는 점원이다.
카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한히 존재한다고 가정한다.
손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러줘야 할 동전의 최소 개수를 구하라.
단, 거슬러 줘야 할 돈 N은 항상 10의 배수이다.

그리디 알고리즘은 최적의 해를 찾는 데 유용하지는 않음.
이 문제의 경우 큰 화폐의 경우 작은 단위의 화폐의 배수기에 큰 화폐부터 처리할 수 있었던 것이다.
그리디 알고리즘 문제에서는 이처럼 문제 풀이를 위한 최소한의 아이디어를 떠올리고 이것이 정당한지 검토할 수 있어야 답을 도출할 수 있다.
이 책의 첫 문제기에 난도가 높진 않았습니다. 그리디 알고리즘에 대해 직관적으로 알 수 있는 예제였습니다.
3-2. 큰 수의 법칙
다양한 수로 이루어진 배열이 있을 때 주어진 수들을 M번 더하여 가장 큰 수를 만든다.
단, 배열의 특정한 인덱스에 해당하는 수가 연속적으로 K번을 초과하여 더해질 수 없는 것이 이 법칙의 특징이다.
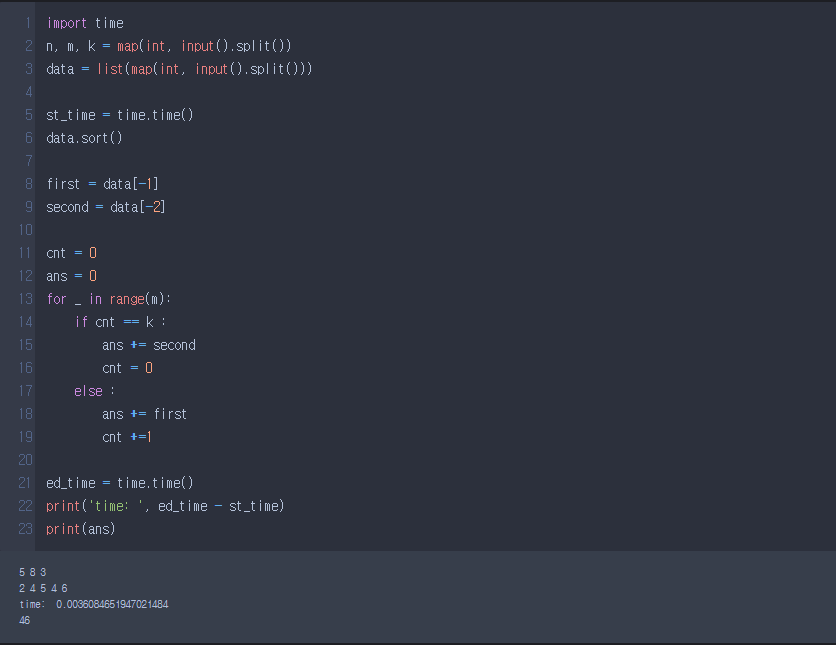
어차피 가장 큰 수를 만들기 위해서는 배열 중 가장 큰 수와 2번째로 큰 수만 사용한다.
고로 first를 K번 썼을 경우에만 second를 한번 사용해주면 해결.
이 경우 M이 10,000 이하이므로 간단히 해결되지만 100억 이상 커질 경우 시간 초과가 생길 수 있다.
조금 더 수학적으로 접근해보자. 가장 큰 수가 K번 - 두 번째 수가 1번, 반복되는 순열을 가짐을 알 수 있다.
순열 seq = K * first + second, 그러므로 int(M/(K+1)) * seq + M % ( K + 1) * K 가 정답이 된다.
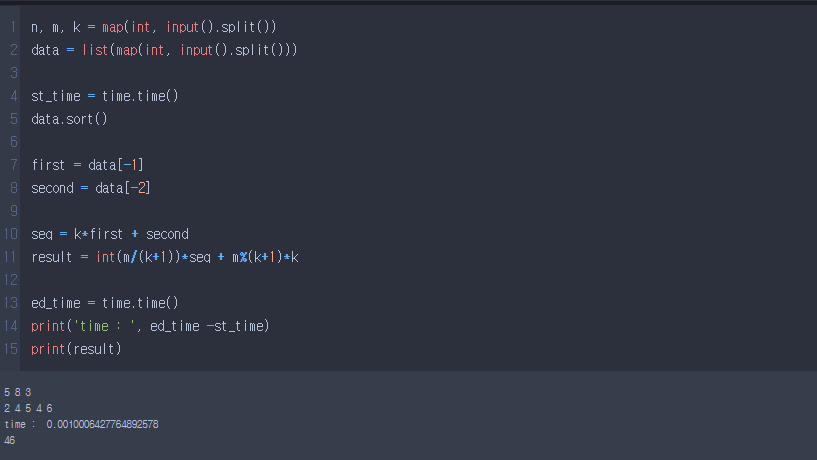
저도 처음에는 첫 번째 코드처럼 작성했습니다. 2번째 코드의 설명을 듣고 '너무 코드를 직관적으로만 써 내려가고 있었구나, 간단한 수학으로 훨씬 코드도 짧아지고 시간도 줄일 수 있구나.'를 느꼈습니다.
뒤통수를 한 대 맞은 듯한 기분이었습니다. 조금 더 다양한 시각에서 접근해보겠습니다. 화이팅!!
3-3. 숫자 카드 게임
여래 개의 숫자 카드 중에서 가장 높은 숫자가 쓰인 카드 한 장을 뽑는 게임이다.
- 숫자가 쓰인 카드들이 N X M 형태로 놓여 있다. 이때 N은 행의 개수를 의미하며, M은 열의 개수를 의미한다.
- 먼저 뽑고자 하는 카드가 포함되어 있는 행을 선택한다.
- 그다음 선택된 행에 포함된 카드들 중 가장 숫자가 낮은 카드를 뽑아야 한다.
- 따라서 처음에 카드를 골라낼 행을 선택할 때, 이후에 해당 행에서 가장 숫자가 낮은 카드를 뽑을 것을 고려하여 최종적으로 가장 높은 숫자의 카드를 뽑을 수 있도록 전략을 세워야 한다.

각 행마다 가장 작은 수를 찾은 후 그중에서 가장 큰 수를 찾는 알고리즘을 찾자.
처음에는 문제를 이해를 못했습니다. 문제를 이해한 후에는 간단하게 해결할 수 있었고, 성급하게 코드를 써 내려가는 것보다 천천히 문제를 알아보고 해결법을 고민해보는 게 조금 더 빠를 수 있다는 걸 느낄 수 있었습니다.
3-4. 1이 될 때까지
어떠한 수 N이 1이 될 때까지 다음의 두 과정 중 하나를 반복적으로 선택하여 수행하려고 한다.
단, 두 번째 연산은 N이 K로 나누어 떨어질 때만 선택할 수 있다.
- N에서 1을 뺀다.
- N을 K로 나눈다.


아직까지도 저는 첫 번째 직관적인 코드가 더 와 닿긴 합니다. N이 100억 이상의 큰 수 일 때 후자의 코드가 더 빠르게 동작한다고 합니다. 이 책을 끝낸 후의 저의 생각이 어떻게 달라질지 궁금해지는 하루입니다. (2021.04.16)
간단한 그리드 알고리즘을 통해 코딩 테스트에 친숙하게 한 걸음 다가갈 수 있었습니다.
3-2 예제에서 간단한 수학으로 짧아지는 코드를 보며 수학과로써 뿌듯함을 느꼈습니다.
앞으로의 코드들은 조금 더 어려워질 테니 걱정 반 기대 반입니다.
Chapter4에서 뵙겠습니다. :)
'Coding > Coding Test & Algorithm' 카테고리의 다른 글
| [SQL] DB(데이터베이스)의 data를 csv로 추출하는 법 (0) | 2021.05.04 |
|---|---|
| [이것이 취업을 위한 코딩 테스트다 with 파이썬] (한빛미디어, 나동빈) Chapter5(3). DFS/BFS (0) | 2021.04.28 |
| [이것이 취업을 위한 코딩 테스트다 with 파이썬] (한빛미디어, 나동빈) Chapter5(2). DFS/BFS (2) | 2021.04.23 |
| [이것이 취업을 위한 코딩 테스트다 with 파이썬] (한빛미디어, 나동빈) Chapter5(1). DFS/BFS (0) | 2021.04.22 |
| [이것이 취업을 위한 코딩 테스트다 with 파이썬] (한빛미디어, 나동빈) Chapter4. 구현 (0) | 2021.04.21 |




