호기심 많은 분석가
[BoostCamp] Week2_Day10. 딥러닝의 기본을 알다. 본문
부스트캠프
개발자의 지속 가능한 성장을 위한 학습 커뮤니티
boostcamp.connect.or.kr
개요
2주 차가 끝나면서, 이번 주는 정말 시간이 모자랐다. 딥러닝에 대해 거의 처음부터 배웠는데, 그동안 궁금했던 점들이 해소돼서 좋았다. 오늘은 그 유명한 GAN에 대해서 배웠는데 참 놀라운 모델이야. 수업을 들으면서 역시 논문을 자주 읽는 버릇을 들여야겠다고 다짐해본다.
개인학습
(09강) Generative Models 1
- 생성 모델 - 대표적으로 GAN이 있다.
Introduction
- What does it mean to learn a generative model?
- generative model은 단순히 GAN이나 VAE를 가지고 문장을 만들거나 이미지를 만드는 것만이 아니다.
- Generative Model이 무엇일까, 어떤 의미를 갖고 있고, GAN은 Generative Model이라는 Category속에서 어떤 방법론에 속하지?라는 체계를 잡는데 도움이 됐으면 좋겠다.
Stanford University CS236: Deep Generative Models
Course Description Generative models are widely used in many subfields of AI and Machine Learning. Recent advances in parameterizing these models using deep neural networks, combined with progress in stochastic optimization methods, have enabled scalable m
deepgenerativemodels.github.io
Learning a Generative Model

- Suppose we are given images of dogs.
- We want to learn a probability distribution $p(x)$ such that
- Generation : if we sample $x_{new} \sim p(x),x_{new}$ should look like a dog (sampling)
- 우리가 하고 싶은 것은 강아지를 Sampling하는 모델을 만드는 것일 수 있다. GAN처럼 서로 다른 강아지를 찍어내는
- Density estimation : $p(x)$ should be high if x looks like a dog, and low otherwise (anomaly detection)
- 이미지가 주어졌을 때 강아지 같은 지 고양이 같은 지, 강아지가 아닌 것 같은 지
- Also known as, explicit models.
- 입력이 주어졌을 때 이것에 대한 확률 값을 얻어낼 수 있는 모델을 explicit models이라 부른다.
- Unsupervised representation learning : We should be able to learn what these images have in common, e.g., ears, tail, etc (feature learning)
- 강아지라면 발이 4개고, 귀가 2개고, 입이 튀어나와 있는 그런 사람과는 다른 특징들이 있다.
- Then, how can we represent $p(x)$?
Basic Discrete Distributions
- Bernoulli distribution : (biased) coin flip - 0 또는 1이 나오는 것
- 얘를 표현하는 분포는 숫자가 1개 필요함, 이 숫자가 되게 중요함
- $D= {Heads,Tails}$
- Specify $P(X=Heads)=p.\ Then P(X=Tails)=1-p$
- Write : $X\sim Ber(p)$
- 왜 biased일까? unbiased일 경우는 $\frac{1}{2}$일 것, 편향된 동전일 때의 확률을 바라본 것이다.
- Categorical distribution : (biased) m-sided dice - 주사위
- 얘를 표현하는 숫자는 m-1개 필요함. 나머지 1개는 기존의 5개로 표현 가능
- $D={1,\cdots,m}$
- Specify $P(Y=i)=p_i,\ such\ that\ \sum_{i=1}^mp_i=1.$
- Write : $Y\sim Cat(p_1,\cdots,p_m)$
Example
- Modeling an RGB joing distribution (of a single pixel)
- rgb image 1개를, pixel 1개를 표현하는데 몇 개의 파라미터가 필요할까?
- $(r,g,b)\sim p(R,G,B)$
- Number of cases?
- r, g, b는 각각 independent 하고, 0~255까지 256개의 값을 가질 수 있음
- $256\times256\times256$
- How many parameters do we need to specify?
- $256\times256\times256-1$
- 하나의 rgb pixel을 fully describe 하기 위해선 필요한 parameter의 숫자가 엄청 많다는 것을 이야기하고 싶다.

Example

- Suppose we have $X_1, \cdots,X_n$ of n binary pixels (a binary image).
- How many possible states?
- $2\times2\times\cdots\times2=2^n$
- 28x28 pixel로 이루어진 이미지라면 $2^{784}$개의 경우의 수가 있다.
- Sampling from $p(x_1,\cdots,x_n)$ generates an image
- How many parameters to specify $p(x_1,\cdots,x_n)$?
- $2^n-1$
Structure Through Independence
- 이 N개의 pixel들이 independent 하다고 가정을 하자
- What if $X_1, \cdots,X_n$ are independent, then
$p(x_1,\cdots,x_n)=p(x_1)p(x_2)\cdots p(x_n)$ - How many possible state? $2^n$
- How many parameters to specify $p(x_1,\cdots,x_n)?$ $n$
- 독립적이니까, 각각의 확률은 1개로도 표현할 수 있다. 그게 n개 있으니까 parameter는 n개 필요한 것
- $2^n$ entries can be described by just $n$ numbers! But this independence assumption is too strong to model useful distributions
- $2^n$개의 파라미터를 n개로 줄였다. Independence assumption이 정말 강력한 assumption이구나
Conditional Independence
- 그 중간쯤을 찾고자 한다. Fully dependent 하면 너무 많은 parameter가 필요하고, 얘를 independent 하자니 parameter는 줄어서 좋은데 표현할 수 있는 이미지가 적어짐
- Three important rules
- Chain rule :
$p(x_1,\cdots,x_n)=p(x_1)p(x_2|x_1)P(x_3|x_1,x_2)\cdots p(x_n|x_1,\cdots,x_{n-1})$- n개의 joint distribution을 n개의 condition distribution으로 바꾸는 것
- $x_i,x_j$가 independent이든, dependent이든 상관없음, 항상 만족하는 것
- Bayes` rule : $p(x|y)=\frac{p(x,y)}{p(y)}=\frac{p(y|x)p(x)}{p(y)}$, 얘도 항상 만족한다.
- Conditional independence : if $x\bot y|z,$ then $p(x|y,z)=p(x|z)$, 얘는 가정임
- z가 주어졌을 때, x와 y가 independent하다(x, y, z 모두 random variable). 그러면 z라는 random variable이 주어졌을 때 x, y가 independent하니까 x라는 random variable을 표현하는 데 있어서 y는 상관이 없다.
- Chain rule에서 뒷단의 컨디션 부분을 날릴 수 있게 해줌
- Chain rule :
- 그래서 Chain rule과 Conditional independence 조건을 잘 활용해서 fully dependent와 independent 사이의 좋은 모델을 만들 것이다. → Autoregressive model
Conditional Independence
- Using the chain rule,
$p(x_1,\cdots,x_n)=p(x_1)p(x_2|x_1)P(x_3|x_1,x_2)\cdots p(x_n|x_1,\cdots,x_{n-1})$ - How many parameters?
- $p(x_1)$: 1 parameter (0 또는 1을 가질 수 있음)
- $p(x_2|x_1)$ : 2 parameters (one per $p(x_2|x_1=0)$ and one per $p(x_2|x_1=1)$)
- $x_1$이 0일 때 $x_2$의 확률과 $x_1$이 1일 때 $x_2$의 확률
- $p(x_3|x_1,x_2)$: 4 parameters
- Hence, 1+2+$2^2+\cdots+2^{n-1}=2^n-1$, which is the same as before
- 아무 가정을 하지 않았기에 파라미터 수가 달라질 리가 없음
- Now, suppose $X_{i+1}\bot X_1, \cdots,X_{i-1}|X_i$(Markov assumption) - i+1번째 변수는 바로 직전의 변수(i)에만 depend 한다, then
$p(x_1,\cdots,x_n)=p(x_1)p(x_2|x_1)p(x_3|x_2)\cdots p(x_n|x_{n-1})$ - How many parameters? 2n-1
- Hence, by leveraging the Markov assumption, we get exponential reduction on the number of parameters.
- Auto-regressice models leverage this conditional independency
Auto-regressive Model

- Suppose we have 28x28 binary pixels.
- Our goal is to learn $p(x)=p(x_1,\cdots,x_{784})$ over $x\in {0,1}^{784}$
- How can we parametrize $p(x)$?
- Let`s use the chain rule to factor the joint distribution
- $p(x_{1:784})=p(x_1)p(x_2|x_1)p(x_3|x_{1:2})\cdots$
- This is called an autoregressive model - 한 정보가 이전 정보들에 depend 한 것
- Note that we need an ordering of all random variables - 순서를 매긴다는 게 중요함
- 이전 N개의 모델을 고려하는 것을 ARN model이라 한다.
- dependency를 어떻게 주는지에 따라 전체 모델의 structure가 달라짐
NADE : Neural Autoregressive Density Estimator
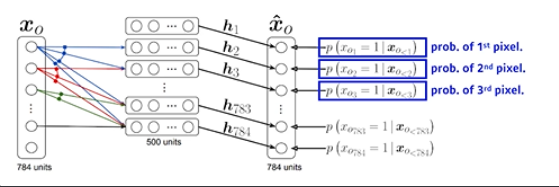
- The probability distribution of i-th pixel is
$p(x_i|x_{1:i-1}=\sigma(\alpha_ih_i+b_i)$ where $h_i=\sigma(W_{<i}x_{1:i-1}+c)$ - NADE is an explicit model that can compute the density of the given inputs
- 단순 generative model이 아니라 확률을 계산할 수 있음
- How can we compute the density of the given image?
- Suppose we have a binary image with 784 binary pixels, ${x_1,x_2,\cdots,x_{784}}$
- Then, the joint probability is computed by
$p(x_1,\cdots,x_{784})=p(x_1)p(x_2|x_1)\cdots p(x_{784}|x_{1:783})$ where each conditional probability $p(x_i|x_{1:i-1})$ is computed independently
- 논문 제목에 Density Estimator라고 적혀 있으면 일반적으로 explicit model을 말하는 경우가 많음
- Binary pixel이기 때문에 아웃풋이 sigmoid를 통과해서 나오는데, continuous random variable의 경우 마지막 레이어에 Gaussian mixture 모델을 활용해서 continuous distribution을 만들겠다.
Pixel RNN
- We can also use RNNs to define an auto-regressive model.
- For example, for an nxn RGB image,
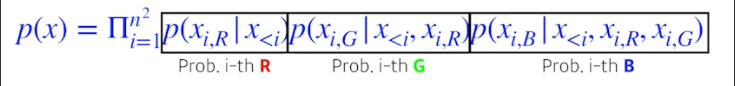
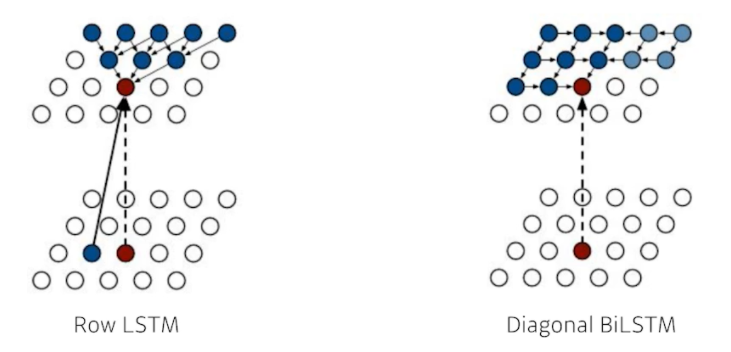
- There are two model architectures in Pixel RNN based on the ordering of chain :
- Ordering 하는 방법에 따라 2가지 모델로 나뉨
- Row LSTM
- R번째 픽셀을 만들 때 위쪽의 정보들을 활용
- Diagonal BiLSTM
- 자기 이전 정보들을 모두 활용한 RNN
- Row LSTM
(10강) Generative Models 2
Latent Variable Models
D. Kingma, "Variational Inference and Deep Learning: A New Synthesis, " Ph.D. Thesis
- 강력 추천, Variational autoencoder와 Adam optimizer를 만든 엄청난 분의 박사학위 논문 - 앞부분만 읽어보기
Question
- Is an autoencoder a generative model?
- 그렇지 않다. 다른 autoencoder와 Variational autoencoder가 어떤 점이 다르기에 generative model이 될 수 있는가를 아는 게 되게 중요하다.
Variational Auto-encoder
Variational-AutoEncoder와 ELBO(Evidence Lower Bound)
안녕하세요. 첫번째 스터디를 위해 글을 올립니다. Variational Auto Encoder Auto-Encoding Variational Bayes, 2014 비록 오래된 논문이긴 하지만 많은 논문에서 VAE의 개념과 사용된 목적함수(Evidence Lower Bound)가
hugrypiggykim.com
- Variational inference (VI)
- 이것이 무엇인지 알기 위해 조금의 수식이 필요하다. 하지만 이 수식을 이해하기 위해서는 오늘 수업뿐만 아니라 논문을 읽어볼 필요가 있다.
- The goal of VI is to optimize the variational distribution that best maches the posterior distribution
- 내가 찾고자 싶은 posterior distribution을 제일 잘 근사할 수 있는 variational distribution을 찾는 이 일련의 과정을 VI라고 한다.
- variational distribution 목적은 posterior distribution을 찾는 데 있다.
- posterior distribution은 나의 observation이 주어졌을 때 내가 관심 있는 random variable의 확률 분포이다. $p_\theta(z|x)$, 여기서 z는 latent vector
- 일반적으로 posterior distribution은 계산이 불가능할 때가 많다. 그래서 얘를 내가 학습할 수 있는, 최적화시킬 수 있는 어떤 것으로 근사하겠다. 이게 목적이고 그 근사하는 분포가 variational distribution이다. $q_\phi(z|x)$
- 그 반대인 $p(x|z)$를 likelihood라고 부름
- In particular, we want to find the variational distribution that minimize the KL divergence between the true posterior
- 그래서 무언가를 잘 찾겠다, 잘 최적화하겠다고 하면 우리에게 필요한 건 loss function이다. 그래서 VI에서는 KL divergence를 이용해서 그 차이를 줄여보겠다는 것

- 우리의 목적은 posterior distribution을 variational distribution으로 찾겠다. 이것 Variational Auto-encoder Encoder에 해당한다.
- But how?

- 내가 지금 posterior distribution이 뭔지도 모르는 데 그것을 근사하는 variational distribution 찾는다는 게 어불성설이다.
- 그걸 가능하게 해 주는 게 VI에 있는 ELBO trick이다.
- 아래를 보면 우리의 목적은 $D_{KL}$(찾고자하는 두 distribution 사이의 거리)을 최소화시키는 게 목적인데 알다시피 그것을 구하는 건 불가능하니까 Evidence Lower Bound라는 좌측 항 ELBO를 키워줌으로써 그것을 해결한다. → 이게 바로 VI이다.
- 이걸 활용해서 Variational Auto-encoder를 학습하는 게 가장 key-idea이다.
- ELBO can further be composed into

- 왼쪽 항이 auto-encoder에서 reconstruction(복원) loss term이 되고 오른쪽이 Prior Fitting Term이 되는 것이다.
- Reconstruction Term : 이것이 Encoder를 통해서 입력 x를 latent space로 보냈다가, 시 decoder로 돌아오는 Reconstruction loss를 줄이는 Term
- Prior Fitting Term : 이미지들이 잔뜩 있는데 이것을 latent space에 잔뜩 올려놨다. 그러면 latent space의 점들이 될 것, 이 점들이 이룬 분포가 내가 가정한 latent space의 prior distribution와 비슷하게 만들어주는 것

- Variational Auto-Encoder는 어떤 입력이 주어지고, 얘를 latent space로 보내서 무언가를 찾고, 걔를 다시 reconstruction 하는 term으로 만들어지는 데 generative model이 되기 위해서는 latent space 된 prior distribution으로 샘플링을 하고 걔를 decoder를 태워서 나오는 아웃풋 도메인 값들이 generation result이다.
- Key limitation :
- It is an intractable model (hard to evaluate likelihood)
- 어떤 모델이 주어졌을 때 얼마나 그럴싸한지 알기가 힘들다.
- The prior fitting term must be differentiable, hence it is hard to use diverse latent prior distribution
- ELBO가 결국 Reconstruction Term과 Prior Fitting Term으로 나누어졌는 데, Reconstruction Term은 뭘 해도 괜찮다. KL divergence라는 Gaussian을 제외하고서는 잘 사용되기 어렵다. 일반적으로 KL divergence를 넣어서 최적화를 시키기 위해서는 미분이 가능해야 하는데, KL divergence는 적분 term을 포함하고 있고, 이 적분이 용이하지 않으면 계산할 수가 없다. 그래서 대부분의 Prior Fitting Term은 Gaussian distribution을 사용한다. → Gaussian이 몇 안 되는 KL divergence의 미분 가능한 form이기 때문
- In most cases, we use an isotropic Gaussian
- isotropic Gaussian은 모든 아웃풋 디멘젼이 independent 한 Gaussian distribution을 의미
- 그럴 경우 아래와 같은 예쁜 식을 따른다.
- 얘를 loss function에 집어넣어서 학습시키면 우리가 원하는 결과가 나온다

Adversarial Auto-encoder
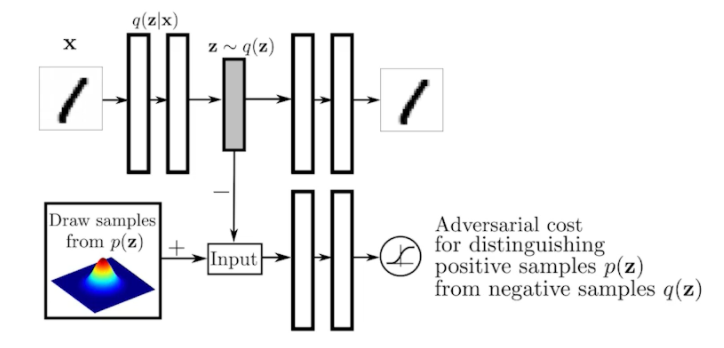
- 앞의 Variational Auto-encoder의 가장 큰 단점은 encoder를 활용할 때 Prior Fitting Term이 KL divergence를 활용하는 것 → 그래서 Gaussian이 아니면 활용하기 힘듦
- 그러나 많은 경우에 Gaussian을 활용하고 싶지 않을 때도 많다.
- It allows us to use any arbitrary latent distribution that we can sample
- GAN을 활용해서 latent distribution 사이의 분포를 맞춰준다.
- Prior Fitting Term을 GAN object로 바꾼 것에 불과함
- 얘는 sampling만 가능한 어떤 구조가 있어도 맞출 수 있다. Ex) Uniform distribution, Gaussian Mixture model,...
- 성능도 Variational Auto-Encoder에 비해 좋을 때가 많다.
- wasserstein autoencoder이라는 논문에서는 Adversarial Auto-encoder가 사실은 latent distribution 사이에 wasserstein distance를 줄여주는 것과 동일한 효과가 있다는 것을 수식적으로 보임. → 그래서 Adversarial Auto-encoder가 wasserstein autoencoder의 한 종류이다.
Generative Adversarial Network (GAN)
I. Goodfellow et al., "Generative Adversarial Networks", NIPS, 2014
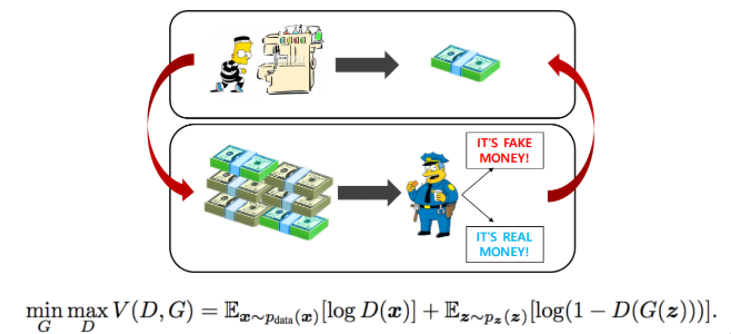
- GAN은 재미있는 아이디어를 가지고 있음, 2-player 게임
- 도둑(generator)이 위조지폐를 만들고 싶어 하는 데, 이걸 잘 분별하는 경찰이 있다. 경찰이 분별한 걸 바탕으로 도둑은 더 경찰을 속이려 하고, 속임을 당하는(discriminator)는 자기가 들고 있는 것과 진짜 지폐를 또 봐서 더 잘 구분하게 만들고, 또 도둑은 더 잘 속이려하고, 이것의 반복 → 궁극적으로 generator의 성능을 높이는 게 GAN의 목적
- GAN의 장점은 내가 학습에 결과로 나오는 generator를 학습하는 discriminator가 점차 점차 좋아지는 것이 가장 큰 장점
- 어떤 fix 된 discriminator를 통해서 generator가 학습하는 것이 아니라, discriminator가 generator에 따라 점점 잘 되기 때문에, 따라서 generator도 성능이 같이 올라가서 굉장히 좋은 이미지를 생성
GAN vs. VAE(Variational Autoencoder)
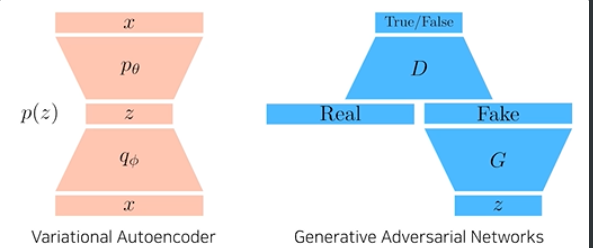
- VAE는 x라는 이미지, 도메인이 들어오면 encoder를 통해서 z로(latent vector) 갔다가 decoder를 통해 다시 x라는 도메인으로 간다. 학습 때 이런 식으로 하고, generation 단계에서는 latent distribution에서 z를 sampling 해서 decoder를 태워서 나오는 x가 출력이 된다.
- GAN은 조금 다르다. z라는 latent distribution에서 출발해서, G(generator)를 통해서 FAKE(가짜)가 나오고, D(discriminator)는 그 FAKE 이미지와 Real 이미지를 구분하는 label(분류기)를 학습하고, generator는 그렇게 학습된 discriminator의 입장에서 True가 나오도록 다시 generator를 업데이트하고, discriminator는 이렇게 해서 결과로 나온 이미지들이 Real 이미지와 discriminate 되도록 다시 학습하고, 이 DG를 반복해서 학습한다.
GAN Objective(목표)
- A two player minmax game between generator and discriminator
- minmax game : 한쪽은 높이고 싶어하고, 한 쪽은 낮추고 싶어 하는 game
- For discriminator :
- 일전의 식에서 G를 두고 D만 본 것
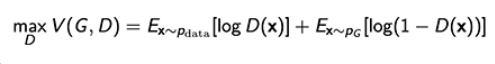
- where the optimal(최상의) discriminator is
- D가 아래의 식과 같을 때 최적화된다. $P_G$는 P_generator
- 얘가 높으면 True, 낮으면 False
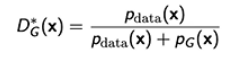
- For generator :

- Plugging in the optimal discriminator, we get
- 아까 찾은 optimal discriminator를 다시 대입하게 되면, 아래 그림과 같은 Jenson-Shannon Divergence가 나오게 된다.

- 수식으로 어떤 것을 보여주고자 했던 거냐면, GAN의 Objective는 데이터를 실제로 만들었다고 생각하는 무엇인지 모르는 distribution과 내가 학습한 generator 사이에 Jenson-Shannon Divergence를 최소화하는 것이다.
- 엄밀하게 이야기하면 Discriminator가 Optimal이라고 가정했을 때, 그것을 Generator 입장에서 학습하는 데 집어넣은 거기 때문에, 실제로 봤을 때 Discriminator가 Optimal에 수렴한다는 것도 보이기 힘들고, 그렇게 됐을 때 Generator가 저렇게 나오지 않을 수도 있기에, 이론적으로는 말이 되지만 현실적으로 Jenson-Shannon Divergence를 줄인다고 얘기하기에는 의아한 점이 있다.
- 하지만 이와 비슷한 논리가 Adversarial autoencoder를 wasserstein autoencoder로 해석할 때 이용된다. 그래서 알아두면 좋다.
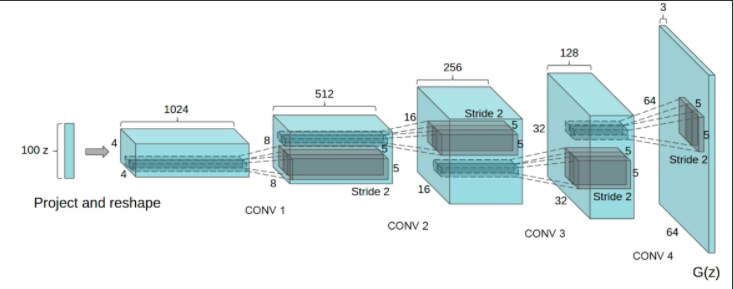
DCGAN
- 기존의 GAN은 MLP, Dense layer를 통해 만들었고, 이것을 이미지 도메인에 deconvolution을 활용해서 한 것이 DCGAN이다.
- 여러 가지 좋은 팁들이 담겨있는 논문
- Ex) 이미지 도메인에서는 당연히 MLP보다 Deconvolution을 활용해서 generate 한 것이 좋더라
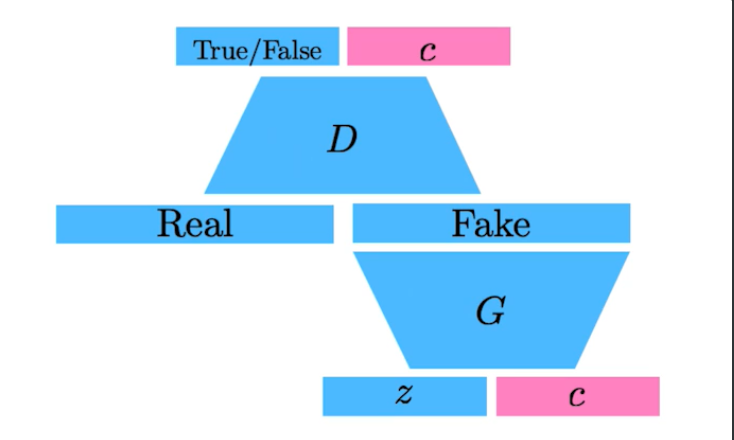
Info-GAN
- 학습할 때 z만 넣는 것이 아니라 c라는 랜덤 한 원 핫 벡터도 같이 넣어줌
- Generation을 할 때 GAN이 특정 모드에 집중할 수 있게 해 줌
- 특정 모드라는 것은 c라는 것으로 나오는 원핫 벡터 또는 컨디셔널 벡터에 집중할 수 있게 해준다.
- 마치 Multi-model distribution 학습하는 것을 c라는 벡터를 통해 약간 잡아주는 효과가 생김
Text2Image
- 문장이 주어지면 이미지를 만든다.
- 이 연구로 시작된 Text2Image로 DALL-E가 탄생

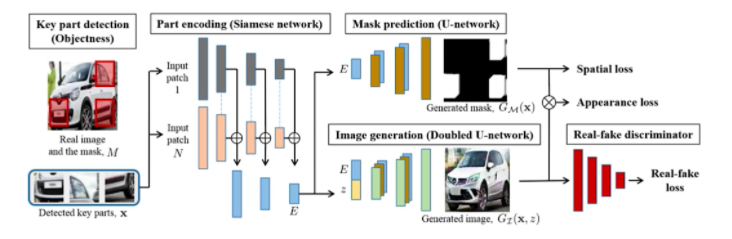
Puzzle-GAN
- 교수님이 저자로 참여하신 GAN
- 이미지 안에 subpatch들이 있다. 자동차라면 헤드라이트, 바퀴, 윈도우 등등
- 이 subpatch들이 들어가면 원래 이미지를 GAN을 통해서 복원하는 모델
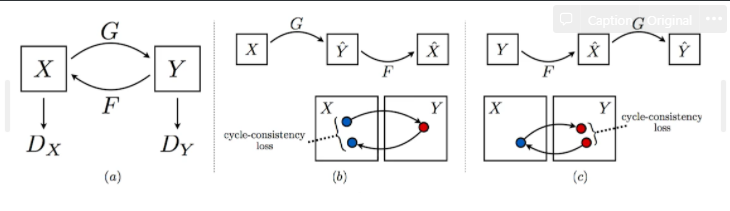
CycleGAN
- GAN 구조를 활용해서 두 개의 도메인을 바꿔줌

- Cycle-consistency loss
- 이것은 굉장히 중요하다. 꼭 알아둬야 하는 Concept
- 이것의 가장 큰 장점은 일반적으로 두 개의 도메인 사이에, 예를 들면 말을 얼룩말로 바꾸기 위해서는 두 개의 똑같은 이미지에 말과 얼룩말이 있는 사진이 필요한데, Cycle-consistency는 굉장히 좋은 게, 야생을 떠도는 수많은 말 사진과, 야생을 떠도는 수많은 얼룩말 사진이 있으면, 임의의 말 사진이 주어졌을 때, 얼룩말 이미지로 바꿔줌
- 이걸 위해 GAN 구조가 2개 들어가 있음
Star-GAN
- Input이 있으면, Gender, Aged, Pale skin 등을 바꿀 수 있음
- 네이버와 고려대학교 학생이 만듦
- 이미지를 내가 컨트롤할 수 있게 만들어줌

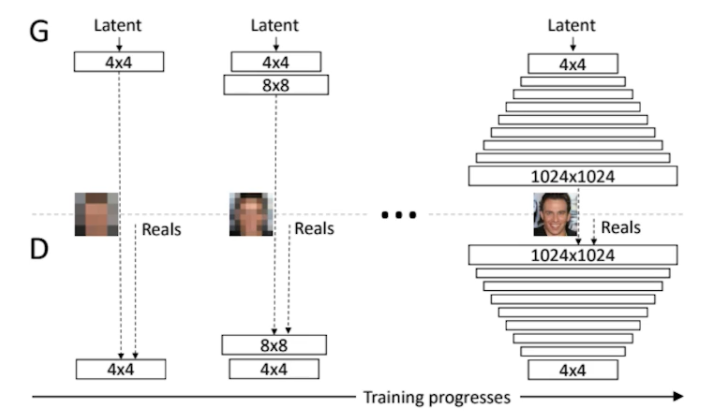
Progressive(진보적인)-GAN
- 고차원의 이미지를 만들 수 있는 GAN
- 이 모델의 가장 큰 특징은 이름에서 알 수 있다시피 처음에는 4x4 pixel에서 시작해서 8x8을 거쳐 마지막에는 1024x1024(HD image)까지 픽셀을 키우는, 한 번에 고차원 이미지를 만들려고 하면 NN이 힘들어하니까 저차원부터 고차원까지 늘려가면서(progressive) 학습을 하면서 굉장히 좋은 성능의 이미지를 만들어낼 수 있었다.

멘토링
- 한 주 소감 나눔
- 기본을 배우고 싶어서 참여했기에, 이번 주는 굉장히 만족스러웠다. 하지만 30분 강의를 정리하는 데 3시간씩 걸려서 시간이 너무 부족했다. 지금도 할게 많아서 아찔하다.
- 다들 각자의 어려움이 많았던 것 같다.
- Google Docs의 Q&A
- Convolution에서 2x2 커널이 안 쓰이는 이유가 궁금합니다. 여러 글들을 찾아보면 관습적으로, 픽셀의 정보를 대칭적으로 뽑을 수 있다, 홀수 커널의 경우 정중앙 픽셀을 특징점으로 쓸 수 있다는 등의 답변들을 봤는데, 이 답변들이 잘 와닿지가 않습니다. 특히 대칭적으로 뽑을 수 있다는 말의 의미를 정확히 모르겠습니다.

- 오른쪽에 있는 두 개의 표가 각각 3x3과 2x2 크기의 커널이라고 생각해봅시다. 3x3 커널은 가운데에 있는 93을 기준점으로 하여, 해당 픽셀의 상하좌우에 있는 픽셀들을 동일하게 대칭적으로 볼 수 있습니다. 하지만 2x2커널의 경우 이렇듯 가운데에 있는 커널 값이 없기 때문에 131,152,104,93 중 하나를 임의로 기준점으로 잡아야 합니다. 이때 131을 기준으로 삼을 경우, convolution 연산을 하는 과정에서 131의 왼쪽 및 위쪽에 있을 픽셀을 고려하지 못하는 단점이 있습니다. 블로그 글의 마지막 즈음에 이러한 내용이 잘 설명되어 있는 것 같습니다.
- FC layer의 경우 input size가 fixed 되는 이유들에 대한 답변입니다. 가장 상위 2개의 대답이 상반되는데 CNN에서 input_size가 fix 되는 이유는 model의 구조 때문인가요?? 13x13x178의 input이 dense layer에서 어떤 과정을 거쳐서 1000개의 output만 출력하는지 과정이 잘 이해가 안 됩니다..
- FC layer가 matrix 형태라서 input size가 달라지면 계산이 안된다. 13x13x178이 2500개가 나온다면 flatten 시켜서, 1x2500 matrix에 FC layer 2500x1000을 해줘서 1x1000개로 1000개의 Class을 뽑아내 준다.
- 그 외 Transformer, MHA 관련 질문들
- 최신 논문들부터 Follow-up 해야 하는 걸까, 예전 것부터 천천히 쌓아야 하는 걸까?
- 옛날 것들을 다 보기엔 시간이 많이 걸리니까 블로그나 개념들만 이해하고 정리해서 넘어가는 게 좋지 않을까, 하지만 보긴 꼭 보는 게 좋다. 그때의 흐름들과 인사이트들을 얻을 수 있으니까
- 멘토링에 하면 좋을 것 의견 제시
- 함께 논문을 읽어보는 시간을 잠깐 가졌으면 좋겠다. 논문 공부하는 방식부터
- 좋은 리뷰가 무엇인가? 모델이 어떤 문제를 해결했는가, 스토리라인을 잘 설명하는 논문
랜덤피어세션
- 각 조의 피어세션 소개
- 22조
- 있었던 질문이나, 참고할만한 자료
- 시간이 남을 때는 각자 카메라 키고 개인 공부
- 40분하고 10분 쉰다
- 멘토님과 소통이 활발함
- 강의를 어려워하는 분이 있으면 허민석, 나동빈 님 리뷰 등을 공유해주심
- 대부분 NLP에 관심이 많다고 하심
- 은행 - 챗봇에 관심 있어서
- 만들고 싶은 product를 생각해보면 조금 더 끌리는 게 있지 않을까요?
- 32조
- 각자 공부하고, 그날 꼭 질문이나 참고할만한 자료나 토이 주제를 준비해와야 함
- 어제는 Attension is all you need 논문 다뤘음, 부스트캠프 끝나고 나서 일을 할 때 어떤 분야가 있는지 찾아보고 정보를 줬음
- 키워드 해서 올리면 미리 질문이나 자료를 올려둠
- 대부분 CV 하신다고 하심
22조 분들이 정리하신 거 보여줬는데 진짜 말도 안 되게 깔끔해서 놀랐다. GitMind라는 프로그램 이용해서 마인드맵 만드신 게 있었는데 되게 인상적이었다.
이것저것 훈훈한 담소 나누면서 마무리함
피어세션
- 팀 회고록 작성
- 다른 팀들 참고해서 좋은 점 추가하고, 아쉬웠던 점 반성
- 이제 전날의 강의를 발표하기로 했기에 준혁님이 RNN, Transformer 강의 리뷰해주심
Q1. short term dependancy 문제?
A. 먼 과거의 데이터가 반영되지 못한다.
Q2. 멀티헤드 어텐션에서 모든 헤드의 아웃풋을 concat 하고 weight를 곱하는 의미?
A. shape을 맞춰주기 위해서.. activation(비선형)도 한번 포함시켜줄 수 있을 것이다.
Q3. 트랜스포머 디코딩이 자기회기적 과정인데, 첫 번째 단어는 어떻게 나오는 것인지?
A. 트랜스포머 구현 튜토리얼 한번 봐보고 다시 얘기하자
Q4. distribution over word?
A. 이제 단어를 뽑을 수 마지막 단계로 보임 - vocabulary size의 one hot vector로 만듦
마스터클래스-최성준님
To Know What We Do Not Know, that is true knowledge
- Sungjoon Choi, Korea Univ
- 전 카카오브레인, 디즈니 리서쳐
- 어떤 것을 말해야 할지 고민돼서 내가 관심 있고 좋아하는 것으로 수업하겠다.
- 이것이 Master... Class
Introduction
무엇을 모르는지 이야기하는 것이 굉장히 어렵다
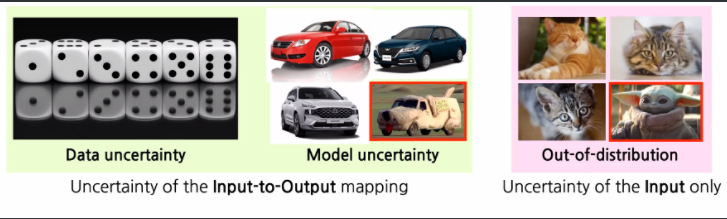
- There are roughly three different types of uncerainties
- Data uncertainty (aleatoric uncertainty)
- 다음번에 나올 주사위 숫자가 무엇인지 모름, 얼마나 어떻게 학습하더라도
- Model uncertainty (epistemic uncertainty)
- 한 번도 본 적 없는 자동차, 데이터가 부족하거나 등으로 모를 때
- Out-of-distribution (novelty detection)
- 한 번도 본 적 없는 타입
- Data uncertainty (aleatoric uncertainty)
세 가지가 완벽하게 나뉘지는 않음
MC-Dropout
Yarin Gal, "Uncertainty in Deep Learning", Thesis, 2016
Papers with Code - Yarin Gal
Papers by Yarin Gal with links to code and results.
paperswithcode.com
- What is Bayesian in Bayesian deep learning?
- 내가 관심 있는 대상의 분포를 찾는다.
Deep Ensembles
Bayesian Computer Vision
"What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision, " 2017
불확실성을 키우는 것이 로스를 줄인다는 게 불확실하다는 걸 인정하고 학습 시에 덜 본다
Confidence Calibration
"On Calibration of Modern Neural Networks, " 2017
예측할 때 내가 맞출 확률에 Confidence도 예측하는 것
- Uncertancy와 정확히 맞닿아 있다.
Max-Softmax
softmax로 통과한 값을 내 confidence 값으로 보자
- 바로 계산하니 안 좋아서 조금 바꿔주니 좋아졌다.
Mixture Density Network
- 교수님 논문
RaPP
- 교수님의 친구가 제1 저자
Deep Deterministic Uncertainty (DDU)
- 굉장히 혁신적임, 관심 있다면 꼭 읽어볼 것
Q. 교수님은 논문을 어떤 방법으로 읽으시나요?
Introduction을 열심히 읽는다.
Q. 구현 팁이 있을까요?
왕도는 없고 계속 구현해봐야 안다. 구현해봐야 논문을 이해할 수 있다.
Q. 제대로 학습만 할 수 있다면 파라미터가 많을수록 좋다.
Scaling Laws for Neural Language Models
We study empirical scaling laws for language model performance on the cross-entropy loss. The loss scales as a power-law with model size, dataset size, and the amount of compute used for training, with some trends spanning more than seven orders of magnitu
arxiv.org
[AI Tech]Daily Report
Naver AI Tech BoostCamp 2기 캠퍼 허정훈 2021.08.03 - 2021.12.27 https://bit.ly/3oC70G9
www.notion.so
'Coding > BoostCamp' 카테고리의 다른 글
| [BoostCamp] Data_Viz_1. 시각화의 기본, Bar Plot (0) | 2021.08.15 |
|---|---|
| [BoostCamp] Data_Viz_1. Data Visualization Introduction (0) | 2021.08.15 |
| [BoostCamp] Week2_Day9. "Key"word. Transformer (0) | 2021.08.14 |
| [BoostCamp] Week2_Day8. 피어세션 때 발표를 하다. (0) | 2021.08.12 |
| [BoostCamp] Week2_Day7. CV vs. NLP 선택의 기로 (0) | 2021.08.12 |




